
如图,一条小船从港口A出发,沿北偏东40°方向航行20海里后到达B处,然后又沿北偏西30°方向航行10海里后到达C处.问此时小船距港口A多少海里(结果精确到1海里)?(参考数据:sin40°=0.6428,cos40°=0.7660,tan40°=0.8391,![]() ≈1.73.)
≈1.73.)
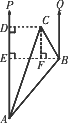
|
分析:要求小船距港口A多少海里,即求AC的长,可过点C作CD⊥AP,构造Rt△ACD,只要求出AD与CD的长,用勾股定理即可求出AC的长. 解:过点B作BE⊥AP,垂足为点E,过点C分别作CD⊥AP,CF⊥BE,垂足分别为点D、F,则四边形CDEF为矩形. 所以CD=EF,DE=CF. 因为∠QBC=30°, 所以∠CBF=60°. 在Rt△BAE中,因为AB=20,∠BAD=40°, 所以AE=AB·cos40°≈20×0.7660≈15.3, BE=AB·sin40°≈20×0.6428≈12.9. 在Rt△BCF中,因为BC=10,∠CBF=60°, 所以CF=BC·sin60°≈10×0.8660≈8.7, BF=BC·cos60°=10×0.5=5. 所以CD=EF=BE-BF≈12.9-5=7.9. 因为DE=CF≈8.7, 所以AD=DE+AE≈8.7+15.3=24.0. 在Rt△ACD中,由勾股定理,得 AC= 即此时小船距港口A约25海里. |


 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:
 0°≈0.6428,cos40°≈0.7660,tan40°≈0.8391,
0°≈0.6428,cos40°≈0.7660,tan40°≈0.8391,| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
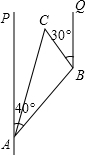
如图,一条小船从港口![]() 出发,沿北偏东
出发,沿北偏东![]() 方向航行
方向航行![]() 海里后到达
海里后到达![]() 处,然后又沿北偏西
处,然后又沿北偏西![]() 方向航行
方向航行![]() 海里后到达
海里后到达![]() 处.问此时小船距港口
处.问此时小船距港口![]() 多少海里?(结果精确到1海里)
多少海里?(结果精确到1海里)
 友情提示:以下数据可以选用:
友情提示:以下数据可以选用:![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:初中数学 来源:第1章《直角三角形的边角关系》中考题集(28):1.4 船有触角的危险吗(解析版) 题型:解答题
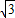 ≈1.732)
≈1.732)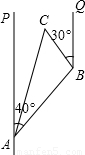
查看答案和解析>>
科目:初中数学 来源:第7章《锐角三角函数》中考题集(46):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
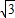 ≈1.732)
≈1.732)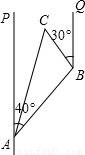
查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《锐角三角函数》(08)(解析版) 题型:解答题
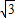 ≈1.732)
≈1.732)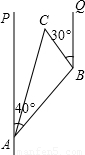
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com