
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=﹣1,下列结论不正确的是( )
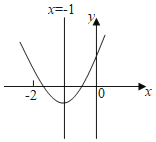
A.b2>4acB.abc>0
C.a﹣c<0D.am2+bm≥a﹣b(m为任意实数)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,与x轴的另一个交点为C,顶点为D,连结CD.
两点,与x轴的另一个交点为C,顶点为D,连结CD.
(1)求该抛物线的表达式;
(2)点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求![]() 的面积的最大值;
的面积的最大值;
②该抛物线上是否存在点P,使得![]() 若存在,求出所有点P的坐标;若不存在,请说明理由.
若存在,求出所有点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如下表(单位:分):
项目人员 | 阅读能力 | 思维能力 | 表达能力 |
甲 | 93 | 86 | 73 |
乙 | 95 | 81 | 79 |
(1)根据实际需要,公司将阅读、思维和表达能力三项测试得分按3:5:2的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
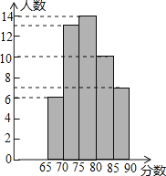
(2)公司按照(1)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值,如最右边一组分数x为:85≤x<90),并决定由高分到低分录用8名员工,甲、乙两人能否被录用?请说明理由,并求出本次招聘人才的录用率.
查看答案和解析>>
科目:初中数学 来源: 题型:
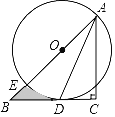
【题目】如图,在![]() 中,∠C=90°,AC=BC,点O在AB上,以O为圆心,OA为半径作⊙O,与BC相切于点D,且交AB于点E.
中,∠C=90°,AC=BC,点O在AB上,以O为圆心,OA为半径作⊙O,与BC相切于点D,且交AB于点E.
(1)连结AD,求证:AD平分∠CAB;
(2)若BE=![]() ﹣1,求阴影部分的面积.
﹣1,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
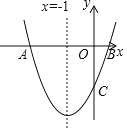
【题目】如图,已知抛物线y=x2+bx+c与x轴交于A、B两点,交y轴于点C,AB=4,对称轴是直线x=﹣1.
(1)求抛物线的解析式及点C的坐标;
(2)连接AC,E是线段OC上一点,点E关于直线x=﹣1的对称点F正好落在AC上,求点F的坐标;
(3)动点M从点O出发,以每秒2个单位长度的速度向点A运动,到达点A即停止运动,过点M作x轴的垂线交抛物线于点N,交线段AC于点Q.设运动时间为t(t>0)秒.
①连接BC,若△BOC与△AMN相似,请直接写出t的值;
②△AOQ能否为等腰三角形?若能,求出t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新学期开始时,某校九年级一班的同学为了增添教室绿色文化,打造温馨舒适的学习环境,准备到一家植物种植基地购买A、B两种花苗.据了解,购买A种花苗3盆,B种花苗5盆,则需210元;购买A种花苗4盆,B种花苗10盆,则需380元.
(1)求A、B两种花苗的单价分别是多少元?
(2)经九年级一班班委会商定,决定购买A、B两种花苗共12盆进行搭配装扮教室.种植基地销售人员为了支持本次活动,为该班同学提供以下优惠:购买几盆B种花苗,B种花苗每盆就降价几元,请你为九年级一班的同学预算一下,本次购买至少准备多少钱?最多准备多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案需要黑色棋子的个数为( )

![]()


A.148B.152C.174D.202
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.

(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
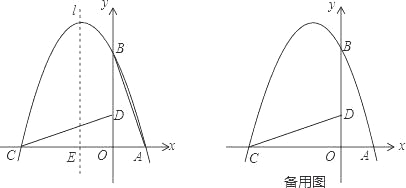
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;
②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com