
【题目】正方形A1B1C1O、A2B2C2C1、A3B3C3C2…按如图的方式放置,点A1,A2,A3…和点C1,C2,C3,…分别在直线 y=x+1 和 x 轴上,则点A2019 的坐标是( )
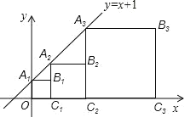
A.(22018 ,22019)B.(22018 1,22018)
C.(22019 ,22018)D.(22018 1,22019 )
【答案】B
【解析】
A1的横坐标为0,把x=0代入y=x+1得:y=1,根据四边形A1B1C1O为正方形,得到A2和B1的横坐标为1,把x=1代入y=x+1得:y=2,即A3的横坐标为1+2=3,把x=3代入y=x+1得:y=4=22,A4的横坐标为1+2+4=7,纵坐标为7+1=8=23,猜想归纳出点A2019的横坐标,代入y=x+1求出纵坐标,即可得到答案.
A1的横坐标为0,把x=0代入y=x+1得:y=1,
∵四边形A1B1C1O为正方形,
∴A2和B1的横坐标为1,把x=1代入y=x+1得:y=2,
即A3的横坐标为1+2=3,把x=3代入y=x+1得:y=4=22,
即A4的横坐标为1+2+4=7,把x=3代入y=x+1得:y=8=23,
…
依此类推,
A2019的纵坐标为22018,把y=22018代入y=x+1得:x=22018-1,
即点A2019的坐标是(22018-1,22018),
故选:B.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() 为
为![]() 的高线,
的高线,![]() ,以
,以![]() 为底边作等腰
为底边作等腰![]() ,连接
,连接![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于
于![]() 点,下列结论:①
点,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 为等腰三角形;⑤
为等腰三角形;⑤![]() ,其中正确的有( )
,其中正确的有( )
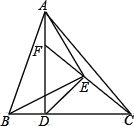
A.①③B.①②④C.①③④D.①②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中∠A、∠B、∠C的对边分别是a、b、c, 下列命题为真命题的是( )
A.如果∠A=2∠B=3∠C,则△ABC是直角三角形
B.如果∠A:∠B:∠C=3: 4: 5,则△ABC是直角三角形
C.如果a: b: c=1: 2: 2,则△ABC是直角三角形
D.如果a: b: c=3: 4: 5,则△ABC是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G, CD=AE.
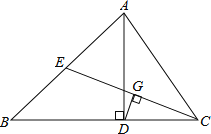
(1)求证: CG=EG.
(2)已知BC=13, CD=5,连结ED,求△EDC 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
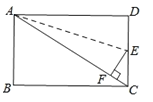
【题目】如图,在长方形ABCD中,AB=6,BC=8.
(1)求对角线AC的长;
(2)点E是线段CD上的一点,把△ADE沿着直线AE折叠.点D恰好落在线段AC上,与点F重合,求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晓东在解一元二次方程时,发现有这样一种解法:如:解方程x(x+4)=6.
解:原方程可变形,得[(x+2)﹣2][(x+2)+2]=6.(x+2)2﹣22=6,(x+2)2=6+22,(x+2)2=10.直接开平方并整理,得![]() ,
,![]() .我们称晓东这种解法为“平均数法”.
.我们称晓东这种解法为“平均数法”.
(1)下面是晓东用“平均数法”解方程(x+2)(x+6)=5时写的解题过程.
解:原方程可变形,得
[(x+□)﹣〇][(x+□)+〇]=5.
(x+□)2﹣〇2=5,
(x+□)2=5+〇2.
直接开平方并整理,得x1=☆,x2=¤.
上述过程中的“□”,“〇”,“☆”,“¤”表示的数分别为 , , , .
(2)请用“平均数法”解方程:(x﹣3)(x+1)=5.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD与BC相交于点O,AC⊥BC于点C,BD⊥AD于点D,添加下列条件中的一个条件:其中能够使△ABC≌△BAD的条件的个数有( )
(1)AC=BD ;(2)OC=OD ;(3)∠CAO=∠D B O ;(4)∠CAB=∠D B A
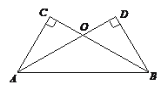
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,位于![]() 处的海上救援中心获悉:在其北偏东
处的海上救援中心获悉:在其北偏东![]() 方向的
方向的![]() 处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东
处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东![]() 相距
相距![]() 海里的
海里的![]() 处救生船,并通知救生船,遇险船在它的正东方向
处救生船,并通知救生船,遇险船在它的正东方向![]() 处,现救生船沿着航线
处,现救生船沿着航线![]() 前往
前往![]() 处救援,若救生船的速度为
处救援,若救生船的速度为![]() 海里/时,请问:
海里/时,请问:

![]() 到
到![]() 的最短距离是多少?
的最短距离是多少?
![]() 救生船到达
救生船到达![]() 处大约需要多长时间?(结果精确到
处大约需要多长时间?(结果精确到![]() 小时:参考数据:
小时:参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com