
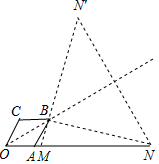
 如图,OM=2,MN=6,A为射线ON上的动点,以OA为一边作内角∠OAB=120°的菱形OABC,则BM+BN的最小值为( )
如图,OM=2,MN=6,A为射线ON上的动点,以OA为一边作内角∠OAB=120°的菱形OABC,则BM+BN的最小值为( )| A. | $\sqrt{26}$ | B. | 6 | C. | 2$\sqrt{13}$ | D. | 2$\sqrt{15}$ |
分析 作N关于直线OB的对称点N′,连接N′M交OB于B,则MN′=BM+BN的最小值,过N′作N′H⊥ON于H,解直角三角形即可得到结论.
解答 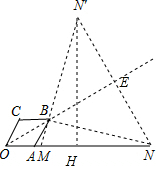 解:∵四边形OABC是菱形,∠OAB=120°,
解:∵四边形OABC是菱形,∠OAB=120°,
∴∠AOC=60°,
∴∠AOB=30°,
作N关于直线OB的对称点N′,连接N′M交OB于B,
则MN′=BM+BN的最小值,
过N′作N′H⊥ON于H,
∵NN′⊥OB于E,
∴∠OEN=90°,
∵∠AOB=30°,
∴∠ONE=60°,
∵OM=2,MN=6,
∴EN=$\frac{1}{2}$ON=4,
∴NN′=8,
∴HN=4,N′H=4$\sqrt{3}$,
∴MH=2,
∴MN′=$\sqrt{M{H}^{2}+HN{′}^{2}}$=2$\sqrt{13}$,
∴BM+BN的最小值为2$\sqrt{13}$,
故选C.
点评 本题考查了轴对称-最小距离问题,菱形的性质,解直角三角形,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
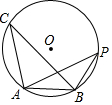 如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为( )
如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为( )| A. | 5 | B. | $\frac{5\sqrt{3}}{2}$ | C. | 5$\sqrt{2}$ | D. | 5$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥1 | B. | x≥1且x≠3 | C. | x≠3 | D. | 1≤x≤3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
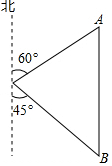 如图,小明家在学校O的北偏东60°方向,距离学校80米的A处,小华家在学校O的南偏东45°方向的B处,小华家在小明家正南方向,求小华家到学校的距离.(结果精确到1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
如图,小明家在学校O的北偏东60°方向,距离学校80米的A处,小华家在学校O的南偏东45°方向的B处,小华家在小明家正南方向,求小华家到学校的距离.(结果精确到1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com