
 如图,某建筑物BC上有一旗杆AB,小明在F处,由E点观察到旗杆顶部A的仰角为52°,底部B的仰角为45°,小明的观测点与地面距离EF为1.6m,旗杆AB长3.15m,求建筑物BC的高度.(结果精确到0.1m)(≈1.414 sin52°≈0.788,tan52°≈1.280)
如图,某建筑物BC上有一旗杆AB,小明在F处,由E点观察到旗杆顶部A的仰角为52°,底部B的仰角为45°,小明的观测点与地面距离EF为1.6m,旗杆AB长3.15m,求建筑物BC的高度.(结果精确到0.1m)(≈1.414 sin52°≈0.788,tan52°≈1.280) 分析 在Rt△ADE中,根据正切函数得出 $\frac{AB+BD}{BD}$=$\frac{3.15+BD}{BD}$=1.28,从而求得BD,进而求得BC=BD+DC=12.9.
解答 解:作ED⊥BC于D,易知DE=BD,EF=CD=1.6m,
在Rt△ADE中,∠ADB=90°,∠AED=52°
∴tan∠AED=$\frac{AD}{DE}$=$\frac{AB+BD}{BD}$=$\frac{3.15+BD}{BD}$=1.28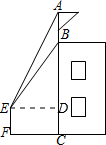
∴BD=11.25(m)
∴BC=11.25+1.6=12.85≈12.9(m).
答:建筑物BC的高度12.9m.
点评 此题考查的知识点是解直角三角形的应用,解题的关键是把实际问题转化为解直角三角形问题,先得到等腰直角三角形,再根据三角函数求解.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
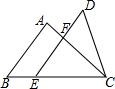 如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=6,EF=4,则DF的长是( )
如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=6,EF=4,则DF的长是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
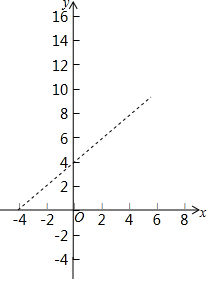 如图,已知 A(-4,0),B(0,4),现以A点为位似中心,相似比为4:9,将OB向右侧放大,B点的对应点为C.
如图,已知 A(-4,0),B(0,4),现以A点为位似中心,相似比为4:9,将OB向右侧放大,B点的对应点为C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com