
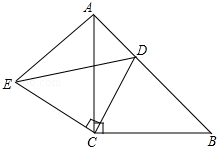
 已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.猜想BD2、AD2、CD2之间的关系,并证明.
已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.猜想BD2、AD2、CD2之间的关系,并证明. 分析 由等腰直角三角形的性质可知BC=AC,CD=CE,∠ACB=∠ECD=90°,通过等量减等量即可推出∠ACE=∠BCD,根据全等三角形的判定定理“SAS”,得到△ACE≌△BCD,BD=AE,∠CAE=∠B=45°,然后根据等腰直角三角形的性质推出∠CAB=45°,即可推出EA⊥BA,即△EAD为直角三角形,再根据勾股定理即可推出AE2+AD2=DE2,即可得到结论.
解答 解:∵△ABC和△ECD都是等腰直角三角形,
∴BC=AC,CD=CE,
∠ACB=∠ECD=90°,
∴∠ACB-∠ACD=∠ECD-∠ACD,
即∠ACE=∠BCD,
在△ACE和△BCD中,
$\left\{\begin{array}{l}{BC=AC}\\{∠ACE=∠BCD}\\{CD=CE}\end{array}\right.$,
∴△ACE≌△BCD(SAS),
∴BD=AE,
∵∠CAE=∠B=45°∠ACE=∠BCD,
∴∠DAE=∠BAC+∠EAC=45°+45°=90°,
∴在Rt△ADE中AD2+AE2=DE2,
即AD2+BD2=DE2,
∵DE=$\sqrt{2}$CD,
∴AD2+BD2=2CD2
点评 本题主要考查全等三角形的判定及性质,勾股定理,等腰直角三角形性质,关键在于认真的阅读题目,正确的运用相关的性质定理求证三角形全等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
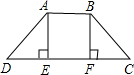 如图,四边形ABCD是一防洪堤坝的横截面,AE⊥CD,BF⊥CD,且AE=BF,∠D=∠C,问AD与BC是否相等?说明你的理由.
如图,四边形ABCD是一防洪堤坝的横截面,AE⊥CD,BF⊥CD,且AE=BF,∠D=∠C,问AD与BC是否相等?说明你的理由.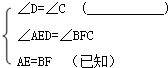
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD、DEFH的边长都是5cm,点P从点D出发,先到点A,然后沿箭头所指方向运动(经过点D时不拐弯),则从出发开始连续运动2014cm时,它离点C 最近,此时它距该点1cm.
如图,正方形ABCD、DEFH的边长都是5cm,点P从点D出发,先到点A,然后沿箭头所指方向运动(经过点D时不拐弯),则从出发开始连续运动2014cm时,它离点C 最近,此时它距该点1cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是一大型广告牌截面,CD是一堵墙的横截面,AB,CD均与地面BE垂直,广告牌的安全拉线ACE要越过围墙(B、D、E三点在同一直线上),已知:AB=5米,CD=3米,∠CED=45°,∠ACE=165°,求拉线ACE的长l(参考数据$\sqrt{2}$≈1.4)
如图,AB是一大型广告牌截面,CD是一堵墙的横截面,AB,CD均与地面BE垂直,广告牌的安全拉线ACE要越过围墙(B、D、E三点在同一直线上),已知:AB=5米,CD=3米,∠CED=45°,∠ACE=165°,求拉线ACE的长l(参考数据$\sqrt{2}$≈1.4)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com