
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,联结
上,联结![]() ,将
,将![]() 绕着点
绕着点![]() 旋转,使得点
旋转,使得点![]() 与边
与边![]() 的中点
的中点![]() 重合,点
重合,点![]() 的对应点是点
的对应点是点![]() ,则
,则![]() 的长等于_____.
的长等于_____.

【答案】![]()
【解析】
如图,延长AB'交BC于E,过点B'作B'D⊥AB于点D,由勾股定理可求AC的长,由旋转的性质可求AP=AM=![]() ,∠PAB=∠CAE,AB=AB'=2,通过证明△ABP∽△CBA,可得∠PAB=∠C,可得CE=AE,由勾股定理可求CE,BE的长,由相似三角形的性质可求B'D,BD的长,即可求解.
,∠PAB=∠CAE,AB=AB'=2,通过证明△ABP∽△CBA,可得∠PAB=∠C,可得CE=AE,由勾股定理可求CE,BE的长,由相似三角形的性质可求B'D,BD的长,即可求解.
如图,延长AB'交BC于E,过点B'作B'D⊥AB于点D,
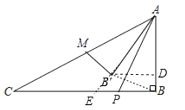
∵∠ABC=90![]() ,AB=2,BC=4,
,AB=2,BC=4,
∴AC=![]() =
=![]() ,
,
∵点M是AC中点,
∴AM=![]() ,
,
∵将△ABP绕着点A旋转,使得点P与边AC的中点M重合,
∴AP=AM=![]() ,∠PAB=∠CAE,AB=AB'=2,
,∠PAB=∠CAE,AB=AB'=2,
∵AP2=AB2+PB2,
∴PB=1,
∴![]() ,又
,又![]()
∴![]()
且∠ABP=∠ABC=90![]() ,
,
∴△ABP∽△CBA,
∴∠PAB=∠C,
∴∠C=∠CAE,
∴CE=AE,
∵AE2=AB2+BE2,
∴CE2=4+(4CE)2,
∴CE=AE=![]() ,
,
∴BE=![]() ,
,
∵B'D∥BC,
∴△AB'D∽△AEB,
∴![]()
∴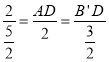 ,
,
∴AD=![]() ,B'D=
,B'D=![]() ,
,
∴BD=AB-AD=2-![]() =
=![]() ,
,
∴BB'=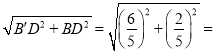
![]()
故答案为:![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人利用扑克牌玩“10点”游戏,游戏规则如下:
①将牌面数字作为“点数”,如红桃6的“点数”就是6(牌面点数与牌的花色无关);
②两人摸牌结束时,将所得牌的“点数”相加,若“点数”之和小于或等于10,此时“点数”之和就是“最终点数”,若“点数”之和大于10,则“最终点数”是0;
③游戏结束之前双方均不知道对方“点数”;
④判定游戏结果的依据是:“最终点数”大的一方获胜,“最终点数”相等时不分胜负.
现甲、乙均各自摸了两张牌,数字之和都是5,这时桌上还有四张背面朝上的扑克牌,牌面数字分别是4,5,6,7.

(1)若甲从桌上继续摸一张扑克牌,乙不再摸牌,则甲获胜的概率为 ;
(2)若甲先从桌上继续摸一张扑克牌,接着乙从剩下的扑克牌中摸出一张牌,然后双方不再摸牌,请用树状图或表格表示出这次摸牌后所有可能的结果,再列表呈现甲、乙的“最终点数”,并求乙获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠XOY=60°,点A在边OX上,OA=2.过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P作PD∥OY交OX于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b的取值范围是_____.
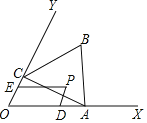
查看答案和解析>>
科目:初中数学 来源: 题型:
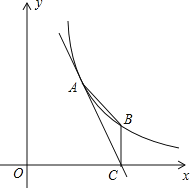
【题目】如图,反比例函数y=![]() (x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线交反比例函数图象于点B.
(x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线交反比例函数图象于点B.
(1)求反比例函数和直线AC的解析式;
(2)求△ABC的面积;
(3)在平面内有点D,使得以A,B,C,D四点为顶点的四边形为平行四边形,请直接写出符合条件的所有D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
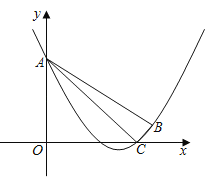
【题目】如图,在平面直角坐标系xOy中,抛物线y=![]() x2+mx+n经过点B(6,1),C(5,0),且与y轴交于点A.
x2+mx+n经过点B(6,1),C(5,0),且与y轴交于点A.
(1)求抛物线的表达式及点A的坐标;
(2)点P是y轴右侧抛物线上的一点,过点P作PQ⊥OA,交线段OA的延长线于点Q,如果∠PAB=45°.求证:△PQA∽△ACB;
(3)若点F是线段AB(不包含端点)上的一点,且点F关于AC的对称点F′恰好在上述抛物线上,求FF′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AD、BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA、CD的延长线相交于点E.
(1)求证:DC是⊙O的切线;
(2)若AE=1,ED=3,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为1的正三角形OAP沿χ轴方向连续翻转若干次,点P依次落在点P1,P2,P3,…,P2018的位置,则点P2018的横坐标为( )
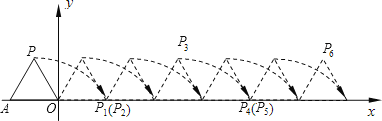
A.2016B.2017C.2018D.2019
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按![]() 元销售时,每天可销售
元销售时,每天可销售![]() 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出![]() 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为![]() 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润![]() 元?
元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com