
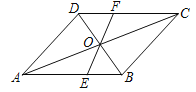
【题目】如图所示,在□ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F.
(1)求证:OE=OF;
(2)若AB=6,BC=5,OE=2,求四边形BCFE的周长.
【答案】(1)证明见解析;
(2)四边形BCFE的周长为15cm.
【解析】试题分析:(1)已知四边形ABCD是平行四边形,根据平行四边形的性质可得OA=OC,AB∥CD,即可得∠OAE=∠OCF,∠OEA=∠OFC,所以△OAE≌△OCF,由全等三角形的性质可得OE=OF;(2)由△OAE≌△OCF,根据全等三角形的性质可得DF=AE,所以BE+CF=AB=6,又因EF=2OE=4,即可得四边形BCFE的周长=BE+BE+CF+EF=6+4+5=15cm.
试题解析:
(1)证明:在□ABCD中,
∵AC与BD相交于点O,
∴OA=OC,AB∥CD,
∴∠OAE=∠OCF,∠OEA=∠OFC,
∴△OAE≌△OCF,
∴OE=OF.
(2)解:∵△OAE≌△OCF,
∴DF=AE,
∴BE+CF=AB=6,
又∵EF=2OE=4,
∴四边形BCFE的周长=BE+BE+CF+EF
=6+4+5=15(cm)


科目:初中数学 来源: 题型:
【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门.
![]()
(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充好电而途中不充电的情况下完成此次任务?请计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为三角形ABD中线, 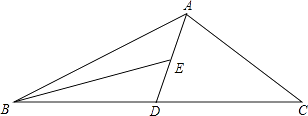
(1)∠ABE=15°,∠BAD=35°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为60,BD=5,则点E到BC边的距离为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,高速公路BC(公路视为直线)的最高限速为120![]() ,在该公路正上方离地面20
,在该公路正上方离地面20![]() 的点A处设置了一个测速仪,已知在点A测得点B的俯角为45°,点C的俯角为30°,测速仪监测到一辆汽车从点B匀速行驶到点C所用的时间是1.5
的点A处设置了一个测速仪,已知在点A测得点B的俯角为45°,点C的俯角为30°,测速仪监测到一辆汽车从点B匀速行驶到点C所用的时间是1.5![]() ,试通过计算,判决该汽车在这段限速路上是否超速.(参考数据:
,试通过计算,判决该汽车在这段限速路上是否超速.(参考数据: ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
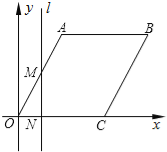
【题目】如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒(0≤t≤4),则能大致反映S与t的函数关系的图象是( )
A.  B.
B. 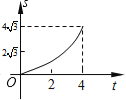
C.  D.
D. 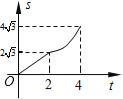
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com