
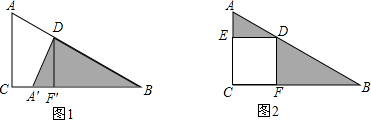
分析 (1)根据旋转的性质,可得答案;
(2)根据旋转的性质,可得∠EDF=∠ADA′=90°,AD=A′D=3,根据三角形的面积公式,可得答案.
解答 (1)解:∵四边形DECF为正方形,
∴∠EDF=90°,DE=DF,
∴DA′绕点D顺时针旋转90度到DA的位置,DF′绕点D逆时针旋转90度到DE位置,
∴图1中的△A′DE′绕点D顺时针旋转90°得到图2;
(2)由旋转的性质,旋转角∠EDF=∠ADA′=90°,AD=A′D=3,
∴∠A′DB=180°-∠ADA′=180°-90°=90°,
∴S△ADE+S△BDF=S△A′BD=$\frac{1}{2}$×A′D×BD=$\frac{1}{2}$×3×4=6,
故答案为:图1中的△A′DE′绕点D顺时针旋转90°得到图2;6.
点评 本题考查了几何变换的类型,利用旋转的性质得出∠EDF=∠ADA′=90°,AD=A′D=3是解题关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com