
【题目】研究发现,地表以下岩层的温度与它所处的深度有表中所示的关系:
岩层的深度 | 1 | 2 | 3 | 4 | 5 | 6 | … |
岩层的温度 | 55 | 90 | 125 | 160 | 195 | 230 | … |
根据以上信息,回答下列问题:
(1)上表反映的两个变量之中,________是自变量,_______是因变量;
(2)岩层的深度![]() 每增加
每增加![]() ,温度
,温度![]() 是怎样变化的?试写出
是怎样变化的?试写出![]() 和
和![]() 的关系式;
的关系式;
(3)估计岩层![]() 深处的温度是多少?
深处的温度是多少?
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则图中与∠DFM相等的角(不含它本身)的个数为( )

A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)如图1,△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线,且B、C在AE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.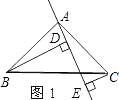
(2)若直线AE绕点A旋转到图2的位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何?请予以证明.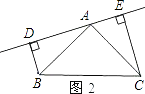
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C;把△BP2C绕点C顺时针旋转180°,得到△CP3D.依此类推,则旋转第2015次后,得到的等腰直角三角形的直角顶点P2016的坐标为( )
A.(4033,﹣1)
B.(4031,﹣1)
C.(4033,1)
D.(4031,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,﹣3),反比例函数![]()
![]() 的图象经过点C.
的图象经过点C.
(1)求反比例函数的解析式;
(2)若点P是反比例函数图象上的一点,△PAD的面积恰好等于正方形ABCD的面积,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),与y轴相交于点C,动点M在线段OA和射线AC上运动.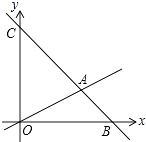
(1)求直线AB的解析式;
(2)若△OMC的面积是△OAC的面积的 ![]() ,请直接写出此时点M的坐标 .
,请直接写出此时点M的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
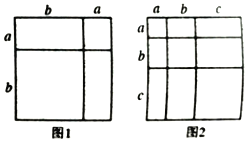
【题目】对于一个图形通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到![]() ,请解答下列问题:
,请解答下列问题:
(1)写出图2中所表示的数学等式;
(2)根据整式乘法的运算法则,通过计算验证上述等a式;
(3)若a+b+c=l0,ab+ac+bc=35,利用得到的结论,求.![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线a:y=2x﹣6,和直线b:y=﹣ ![]() x+4相交于点H,分别与x、y轴交于点A、B、C、D,点P在x轴上,过点P作x轴的垂线,分别与直线a、b交于点E、F.
x+4相交于点H,分别与x、y轴交于点A、B、C、D,点P在x轴上,过点P作x轴的垂线,分别与直线a、b交于点E、F.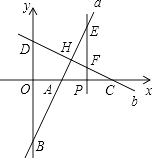
(1)求点H的坐标;
(2)判断直线a、b的位置关系,并说明理由;
(3)设点P的横坐标为m,当m为何值时,以D、E、F、O为顶点的四边形是
平行四边形,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com