



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
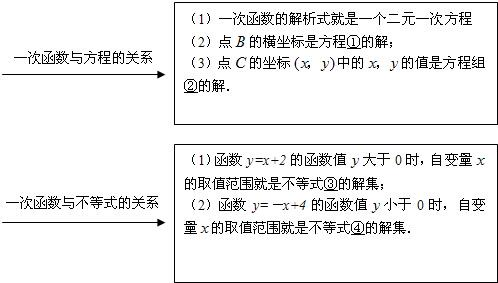
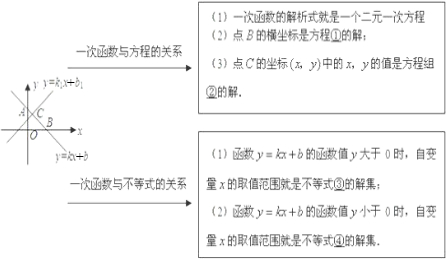
 ����ѧѧϰ�У���ʱ��֪ʶ���й��ɺ������Ǹ���ѧϰ����Ҫ����������ѧϰ��С����ѧϰ��һ�η��̣��飩��һԪһ�β���ʽ��һ�κ��������֪ʶ�����������£�
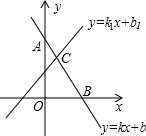
����ѧѧϰ�У���ʱ��֪ʶ���й��ɺ������Ǹ���ѧϰ����Ҫ����������ѧϰ��С����ѧϰ��һ�η��̣��飩��һԪһ�β���ʽ��һ�κ��������֪ʶ�����������£�| ��1��һ�κ����Ľ���ʽ����һ����Ԫһ�η��̣� ��2����B�ĺ������Ƿ��̢ٵĽ⣻ ��3����C�����꣨x��y���е�x��y��ֵ�Ƿ�����ڵĽ⣮һ�κ����벻��ʽ�Ĺ�ϵ��
|