
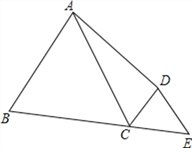
【题目】如图,已知AB=AD,∠BAD=60°,∠BCD=120°,延长BC,使CE=CD,连接DE,求证:BC+DC=AC.
思路点拨:
(1)由已知条件AB=AD,∠BAD=60°,可知:△ABD是 三角形;
(2)同理由已知条件∠BCD=120°得到∠DCE= ,且CE=CD,可知 ;
(3)要证BC+DC=AC,可将问题转化为两条线段相等,即 = ;请你先完成思路点拨,再进行证明:
【答案】(1)等边.(2)60°,△DCE是等边三角形.(3)BE=AC,证明见解析。
【解析】分析:(1)连接BD,根据等边三角形判定推出即可;(2)求出∠DCE=60°,得到等边三角形DCE即可;(3)根据等边三角形性质推出AD=BD,CD=DE,∠ADB=∠CDE=60°,推出∠ADC=∠BDE,证△ADC≌△BDE即可;
本题解析:(1)等边.(2)60°,△DCE是等边三角形.
(3)BE=AC.
证明:连接BD,
∵AB=AD,∠BAD=60°,∴△ABD是等边三角形,
∵∠BCD=120°,
∴∠DCE=180°-∠BCD=180°-120°=60°,
∵CE=CD,
∴△DCE是等边三角形,
∵等边三角形ABD和DCE,
∴AD=BD,CD=DE,∠ADB=∠CDE=60°,
∴∠ADB+∠BDC=∠CDE+∠BDC,
即∠ADC=∠BDE,
在△ADC和△BDE中,AD=BD,∠ADC=∠BDE, DC=DE,
∴△ADC≌△BDE,
∴AC=BE=BC+CE =BC+DC,
∴BC+DC=AC



 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于( )
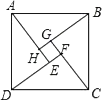
A. 8 B. 6 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】拒绝“餐桌浪费”,刻不容缓.每人一日三餐少浪费一粒米,全国一年就可节省3150万斤,可供9万人吃一年.数据“3150万”用科学记数法表示为( )
A. 0.315×108 B. 3.15×107 C. 31.5×106 D. 315×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个用铁丝围成的篮框,我们来仿制一个类似的柱体形篮框.如图2,它是由一个半径为r、圆心角90°的扇形A2OB2,矩形A2C2EO、B2D2EO,及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn,OEFG围成,其中A1、G、B1在![]() 上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
(1)求d的值;
(2)问:CnDn与点E间的距离能否等于d?如果能,求出这样的n的值,如果不能,那么它们之间的距离是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚准备用自己节省的零花钱购买一台MP5来学习英语,他已存有50元,并计划从本月起每月节省30元,直到他至少有280元.设x个月后小刚至少有280元,则可列计算月数的不等式为( )
A.30x+50>280
B.30x-50≥280
C.30x-50≤280
D.30x+50≥280
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.下图中线段![]() 、
、![]() 分别表示父、子俩送票、取票过程中,离体育馆的路程
分别表示父、子俩送票、取票过程中,离体育馆的路程![]() (米)与所用时间
(米)与所用时间![]() (分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
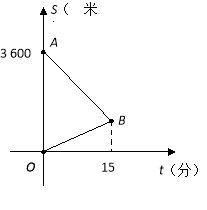
【1】求点![]() 的坐标和
的坐标和![]() 所在直线的函数关系式
所在直线的函数关系式
【2】小明能否在比赛开始前到达体育馆
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解方程3x-5=-x+1中,下面移项正确的是( )
A. 3x+x=5+1 B. 3x-x=-5-1 C. 1-5=-3x+x D. 3x+x=5-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com