练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．随着北京公交票制票价调整，公交集团更换了新版公交站牌，乘客在乘车时可以通过新版公交站牌计算乘车费用．新版站牌每一个站名上方都有一个对应的数字，将上下车站站名所对应数字相减取绝对值就是乘车路程，再按照其所在计价区段，参照票制规则计算票价．具体来说：
    乘车路程计价区段0-1011-1516-20…
    对应票价（元）234…
    另外，一卡通普通卡刷卡实行5折优惠，学生卡刷卡实行2.5折优惠．
    小明用学生卡乘车，上车时站名上对应的数字是5，下车时站名上对应的数字是22，那么，小明乘车的费用是1元．

    分析 首先用下车时站名上对应的数字减去上车时站名上对应的数字，求出小明乘车的路程是多少，进而求出相应的票价是多少；然后用它乘以0.25，求出小明乘车的费用是多少元即可．

    解答 解：因为小明乘车的路程是：22-5=17，
    所以小明乘车的费用是：
    4×0.25=1（元）．
    答：小明乘车的费用是1元．
    故答案为：1．

    点评 此题主要考查了有理数的混合运算，要熟练掌握有理数混合运算顺序：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算，解答此题的关键是求出小明乘车的路程、相应的票价是多少．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．（1）当x=-1时，求分式$\frac{x-1}{{2{x^2}+1}}$的值．
    （2）已知a2-4a+4与|b-1|互为相反数，求$\frac{a-b}{a+b}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．a，b，c是直线，且a∥b，b∥c，则a∥c．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．2015年4月l8日周杰伦“摩天轮2”演唱会在重庆奥体中心如期举行．小王开车从家出发前去观看，预计1个小时能到达，可当天路上较为拥堵，行驶了半个小时，刚好行驶了一半路程，道路被“堵死”，堵了几分钟突然发现旁边刚好有一个轻轨站，于是小王将车停在轻轨站的车库，然后坐轻轨前往，结果按预计时间到达．下面能反映小王距离奥体中心的距离y （千米）与时间x （小时）的函数关系的大致图象是（　　）
    A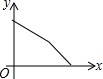．B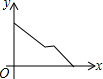．C．D．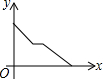

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．阅读材料：
    如图1，在平面直角坐标系中，O为坐标原点，对于任意两点A （x1，y1），B（x2，y2），由勾股定理可得：AB2=（x1-x2）2+（y1-y2）2，我们把$\sqrt{（{x}_{1}-{x}_{2}）^{2}+（{y}_{1}-{y}_{2}）^{2}}$叫做A、B两点之间的距离，记作AB=$\sqrt{（{x}_{1}-{x}_{2}）^{2}+（{y}_{1}-{y}_{2}）^{2}}$
    例题：在平面直角坐标系中，O为坐标原点，设点P（x，0）．
    ①A（0，2），B （3，-2），则AB=5．；PA=$\sqrt{{x}^{2}+4}$．；
    解：由定义有AB=$\sqrt{（0-3）^{2}+[2-（-2）]^{2}}=5$；PA=$\sqrt{（x-3）^{2}+（0-2）^{2}}=\sqrt{{x}^{2}+4}$．
    ②$\sqrt{（x-1）^{2}+4}$表示的几何意义是点P（x，0）到点（1，2）的距
    离；$\sqrt{{x}^{2}+1}+\sqrt{（x-2）^{2}+9}$表示的几何意义是点P（x，0）分别到点（0，1）和点（2，3）的距离和．
    解：因为$\sqrt{（x-1）^{2}+4}=\sqrt{（x-1）^{2}+（0-2）^{2}}$，所以$\sqrt{（x-1）^{2}+4}$表示的几何意义是点P（x，0）到点（1，2）的距
    离；同理可得，$\sqrt{{x}^{2}+1}+\sqrt{（x-2）^{2}+9}$表示的几何意义是点P（x，0）分别到点（0，1）和点（2，3）的距离和．
    根据以上阅读材料，解决下列问题：
    （1）如图2，已知直线y=-2x+8与反比例函数y=$\frac{6}{x}$（x＞0）的图象交于A（x1，y1）、B（x2，y2）两点，
    则点A、B的坐标分别为A（1，6），B（3，2），AB=2$\sqrt{5}$．
    （2）在（1）的条件下，设点P（x，0），则$\sqrt{（x-{x}_{1}）^{2}+{y}_{1}^{2}}+\sqrt{（x-{x}_{2}）^{2}+{y}_{2}^{2}}$表示的几何意义是点P（x，0）分别到点（1，6）和点（3，2）的距离和；试求$\sqrt{（x-{x}_{1}）^{2}+{y}_{1}^{2}}+\sqrt{（x-{x}_{2}）^{2+{y}_{2}^{2}}}$的最小值，以及取得最小值时点P的坐标．

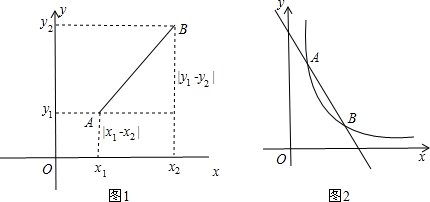
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

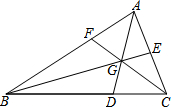    5．已知：如图，在△ABC中，点D，E，F分别在三边上，E是AC的中点，BD=2DC，AD，BE，CF交于一点G，S△BGD=16，S△AGE=6，则△ABC的面积是60．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图是甲、乙两人同一地点出发后，路程随时间变化的图象．
    （1）此变化过程中，时间是自变量，路程因变量；
    （2）甲的速度是$\frac{50}{3}$千米/时，乙的速度是$\frac{100}{3}$千米/时；
    （3）6时表示乙追上甲；
    （4）路程为150千米，甲行驶了9小时，乙行驶了4小时；
    （5）9时甲在乙的后面（前面、后面、相同位置）；
    （6）分别写出甲乙两人行驶的路程s（千米）与行驶的时间t（小时）的函数关系式（不要求写出自变量的取值范围）
    S甲=$\frac{50}{3}$t
    S乙=$\frac{150}{4}$t-$\frac{450}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图，将△ABC沿BC方向平移l个单位，得到△DEF，若四边形ABFD的周长是12，则△ABC的周长为10．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

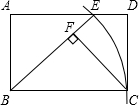    10．如图，AD∥BC，∠BAD=90°，以点B为圆心，BC长为半径画弧，与射线AD相交于点E，连接BE，过C点作CF⊥BE，垂足为F．
    （1）线段BF与图中现有的哪一条线段相等？先将你猜想出的结论填写在下面的横线上，然后再加以证明．结论：BF=AE．
    （2）连结CE，如果BC=10，AB=6，求sin∠ECF的值．

    查看答案和解析>>

    同步练习册答案