
分析 (1)先计算△,化简得到△=(k-2)2,易得△≥0,然后根据△的意义即可得到结论;
(2)利用求根公式计算出方程的两根x1=k-1,x2=1,则可设b=k-1,c=2,然后讨论:当2为腰;当1为腰,分别求出边长,但要满足三角形三边的关系,最后计算周长.
解答 (1)证明:△=k2-4×1×(k-1)
=k2-4k+4
=(k-2)2,
∵无论k取什么实数值,(k-2)2≥0,
∴△≥0,
∴无论k取什么实数值,方程总有实数根;
(2)解:∵x=$\frac{k±(k-2)}{2}$,
∴x1=k-1,x2=1,
∵两边恰好是这个方程的两个实数根,
当2为腰,则k-1=2,解得k=3,此时三角形的周长=2+2+1=5;
当1为腰时,k-1=1,k=2,此时1+1=2,故此种情况不存在.
综上所述,△ABC的周长为5.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了三角形三边的关系以及分类讨论思想的运用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
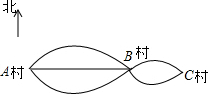 如图,从A村去B村有3条道路,从B村去C村有2条道路.
如图,从A村去B村有3条道路,从B村去C村有2条道路.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com