
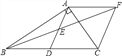
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.
【答案】(1)证明见解析;(2)证明见解析;(3)10.
【解析】试题分析:(1)利用AAS证明全等.(2)利用(1)中结论,先证明ADCF是平行四边形,再利用直角三角形中线性质求相邻边相等.(3)利用菱形面积公式求面积.
试题解析:
解:(1)证明:∵AF∥BC,∴∠AFE=∠DBE,∠FAE=∠BDE.∵E为AD的中点,∴AE=DE,∴△AFE≌△DBE.
(2)证明:由(1)知△AEF≌△DEB,则AF=DB.∵DB=DC,∴AF=CD.∵AF∥BC,∴四边形ADCF是平行四边形.∵∠BAC=90°,D是BC的中点,∴AD=DC=![]() BC,
BC,
∴四边形ADCF是菱形.
(3)连接DF,由(2)知AF∥BD,AF=BD,
∴四边形ABDF是平行四边形,∴DF=AB=5,∴S菱形ADCF=![]() AC·DF=
AC·DF=![]() ×4×5=10.
×4×5=10.


科目:初中数学 来源: 题型:
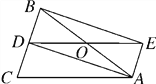
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个粒子在第一象限和x,y轴的正半轴上运动,在第一秒内,它从原点运动到(0,1),接着它按图所示在x轴、y轴的平行方向来回运动,(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…)且每秒运动一个单位长度,那么2010秒时,这个粒子所处位置为( )

A.(14,44) B.(15,44) C.(44,14) D.(44,15)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于A,B两点,点A在点B的左边,与y轴交于点C,顶点为D,若以BD为直径的⊙M经过点C.
(1)请直接写出C,D两点的坐标(用含a的代数式表示);
(2)求抛物线的函数表达式;
(3)在抛物线上是否存在点E,使∠EDB=∠CBD?若存在,请求出所有满足条件的点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
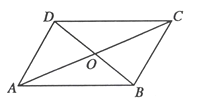
【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD//BC,AC=8,BD=6.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求□ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在面积为12的平行四边形ABCD中,过点A作直线BC的垂线交直线BC于点E,过点A作直线CD的垂线交直线CD于点F,若AB=4,BC=6,则CE+CF的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F;点M是边AB的一个三等分点。则△AOE与△BMF的面积比为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有质地均匀的A、B、C、D四张卡片,上面对应的图形分别是圆、正方形、正三角形、平行四边形,将这四张卡片放入不透明的盒子中摇匀,从中随机抽出一张(不放回),再随机抽出第二张.
(1)如果要求抽出的两张卡片上的图形,既有圆又有三角形,请你用列表或画树状图的方法,求出出现这种情况的概率.
(2)因为四张卡片上有两张上的图形,既是中心对称图形,又是轴对称图形,所以小明和小东约定做一个游戏,规则是:如果抽出的两个图形,既是中心对称图形又是轴对称图形,则小明赢;否则,小东赢.问这个游戏公平吗?为什么?如果不公平,请你设计一个公平的游戏规则.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com