如图，AB//CD,∠CAB=108°，AC=2.
⑴用直尺和圆规作∠A的平分线AE,交CD于E,并在AB
上取一点F，使AC=AF，再连接CF,交AE于K；
（要求保留作图痕迹，不必写出作法）
⑵依据现有条件，直接写出图中所有相似的三角形，并求出AK.
（图中不再增加字母和线段，不要求证明）.
 |
科目：初中数学 来源： 题型：
观察控究，完成证明和填空．
如图，四边形ABCD中，点E、F、G、H分别是边AB、BC、CD、DA的中点，顺次连接E、F、G、H，得到的四边形EFGH叫中点四边形．
（1）求证：四边形EFGH是平行四边形；
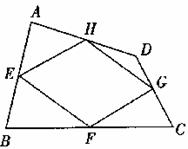
（2）如图，当四边形ABCD变成等腰梯形时，它的中点四边形是菱形，请你探究并填空：
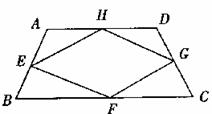
当四边形ABCD变成平行四边形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；
当四边形ABCD变成矩形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；
当四边形ABCD变成菱形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；
当四边形ABCD变成正方形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；
（3）根据以上观察探究，请你总结中点四边形的形状由原四边形的什么决定的？
查看答案和解析>>
科目：初中数学 来源： 题型：
正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线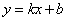
(k＞0)和x轴上，已知点B1(1，1)，B2(3，2)，则Bn的坐标是_____ _________．
 |
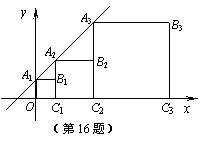查看答案和解析>>
科目：初中数学 来源： 题型：
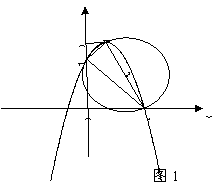
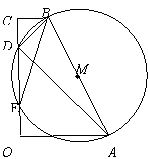
已知：直角梯形OABC中，BC∥OA，∠AOC=90°，以AB为直径的圆M交OC于D．E，连结AD、BD、BE。
(1)在不添加其他字母和线的前提下，直接写出图1中的两对相似三角形。
_____________________，______________________ 。
(2)直角梯形OABC中，以O为坐标原点，A在x轴正半轴上建立直角坐标系（如图2），若抛物线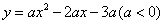
经过点A．B．D，且B为抛物线的顶点。
①写出顶点B的坐标（用a的代数式表示）___________。
②求抛物线的解析式。
③在x轴下方的抛物线上是否存在这样的点P：过点P做PN⊥x轴于N，使得△PAN与△OAD相似？若存在，求出点P的坐标；若不存在，说明理由。
 | |||
 | |||
查看答案和解析>>
科目：初中数学 来源： 题型：
如右图，已知△ABC中，AB＝AC，AD平分∠BAC，请补充完整过程说明△ABD≌△ACD的理由．
解： ∵AD平分∠BAC
∴∠________＝∠_________（角平分线的定义）
在△ABD和△ACD中
∴△ABD≌△ACD（ ）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
………………………………………1分
……………………………………………………………………………………8分
，
，
，若无论
取何值，
总取
、
、
中的最小值，则
的平方根是 （ ）
C. ±4 D.±2
在同一直角坐标系内的图象大致是（ ）