
求证:顺次连结四边形各边中点所得的四边形是平行四边形.
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源:鼎尖助学系列—同步练习(数学 九年级下册)、课题学习——中点四边形(2) 题型:047
求证:顺次连结四边形的各边中点所组成的四边形的面积是原四边形面积的一半.
查看答案和解析>>
科目:初中数学 来源:鼎尖助学系列—同步练习(数学 九年级下册)、课题学习——中点四边形(2) 题型:047
求证:顺次连结四边形的各边中点所组成的四边形的周长等于原四边形两条对角线的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
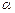 (0°<
(0°<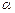 <90°),
<90°),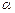 的代数式表示∠HAE= ;(1分)
的代数式表示∠HAE= ;(1分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com