
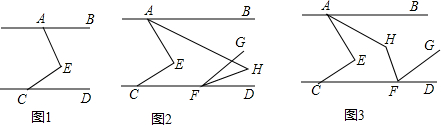
分析 (1)过E作EF∥AB,可得∠A=∠AEF,利用平行于同一条直线的两直线平行得到EF与CD平行,再得到一对内错角相等,进而得出答案;
(2)①HF平分∠DFG,设∠GFH=∠DFH=x,根据平行线的性质可以得到∠AHF的度数;②设∠GFD=2x,∠BAH=∠EAH=y,根据角平分线的性质以及平行线的性质即可得到∠AHF与∠AEC的数量关系.
解答 解:(1)如图1,过点E作直线EN∥AB,
∵AB∥CD,
∴EN∥CD,
∴∠BAE=∠AEN,∠DCE=∠CEN,
∴∠AEC=∠AEN+∠CEN=∠BAH+∠ECD;
(2)∵AH平分∠BAE,
∴∠BAH=∠EAH,
①∵HF平分∠DFG,设∠GFH=∠DFH=x,
又CE∥FG,
∴∠ECD=∠GFD=2x,
又∠AEC=∠BAE+∠ECD,∠AEC=90°,
∴∠BAH=∠EAH=45°-x,
如图2,过点H作l∥AB,
易证∠AHF=∠BAH+∠DFH=45°-x+x=45°;
②设∠GFD=2x,∠BAH=∠EAH=y,
∵HF平分∠CFG,
∴∠GFH=∠CFH=90°-x,
由(1)知∠AEC=∠BAE+∠ECD=2x+2y,
如图3,过点H作l∥AB,
易证∠AHF-y+∠CFH=180°,
即∠AHF-y+90°-x=180°,∠AHF=90°+(x+y),
∴∠AHF=90°+$\frac{1}{2}$∠AEC.(或2∠AHF-∠AEC=180°.)
点评 此题考查了平行线的性质,熟练掌握平行线的性质作出辅助线是解本题的关键.


科目:初中数学 来源: 题型:填空题
 如图所示,在平面直角坐标系中,“鱼”的每个“顶点”都在小正方形的顶点处,点A为“鱼”的一个顶点,将“鱼”向右平移3个单位长度,再向下平移6个单位长度,则平移后点A的坐标为(-1,0).
如图所示,在平面直角坐标系中,“鱼”的每个“顶点”都在小正方形的顶点处,点A为“鱼”的一个顶点,将“鱼”向右平移3个单位长度,再向下平移6个单位长度,则平移后点A的坐标为(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知A(0,2),M(6,4),N(8,8),动点P从点A出发,沿y轴以每秒2个单位长度的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.
如图,在平面直角坐标系中,已知A(0,2),M(6,4),N(8,8),动点P从点A出发,沿y轴以每秒2个单位长度的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,把面积为a的正三角形ABC的各边依次循环延长一倍,顺次连接这三条线段的外端点,这样操作后,可以得到一个新的正三角形DEF;对新三角形重复上述过程,经过2016次操作后,所得正三角形的面积是72016a.
如图,把面积为a的正三角形ABC的各边依次循环延长一倍,顺次连接这三条线段的外端点,这样操作后,可以得到一个新的正三角形DEF;对新三角形重复上述过程,经过2016次操作后,所得正三角形的面积是72016a.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a>b,则a-1>b-1 | B. | 若3a>3b,则a>b | ||
| C. | 若a>b,且c≠0,则ac>bc | D. | 若a>b,则7-a<7-b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com