
����Ŀ��ij�������۹�˾����ijƷ��A�������������������ռ�����۸�Ҳ�ڲ����½�������5�·�A���������ۼ۱�ȥ��ͬ��ÿ������1��Ԫ�����������ͬ������A��������ȥ�����۶�Ϊ100��Ԫ���������۶�ֻ��90��Ԫ��
��1������5�·�A������ÿ���ۼ۶�����Ԫ��
��2��Ϊ���������룬�������۹�˾�����پ���ͬƷ�Ƶ�B����������֪A������ÿ������Ϊ7.5��Ԫ��B������ÿ������Ϊ6��Ԫ����˾Ԥ���ò�����105��Ԫ�Ҳ�����99��Ԫ���ʽ�������������15�����м��ֽ���������
��3�����B������ÿ���ۼ�Ϊ8��Ԫ��Ϊ��B����������·����˾����ÿ�۳�һ��B�������������˿��ֽ�a��Ԫ��Ҫʹ��2�������еķ���������ͬ��aֵӦ�Ƕ��٣���ʱ�����ַ����Թ�˾��������
���𰸡�
��1���⣺�����5�·�A������ÿ���ۼ�m��Ԫ����
![]() ��
��
��ã�m=9��
�����飬m=9��ԭ���̵ĸ��ҷ������⣮
�𣺽���5�·�A������ÿ���ۼ�9��Ԫ
��2���⣺�蹺��A������x������
99��7.5x+6��15��x����105��
��ã�6��x��10��
��x����������Ϊ6��7��8��9��10��
���5�ֽ�������
��3���⣺���ܻ���ΪW��Ԫ������A������x������
W=��9��7.5��x+��8��6��a����15��x��=��a��0.5��x+30��15a��
��a=0.5ʱ����2�������з���������ͬ��
��ʱ������A������6����B������9��ʱ�Թ�˾������
����������1���ۣ��ܼ����ԣ�Ӧ�����������е�����ϵ��������ϵΪ���������������=ȥ���������������2����ϵʽΪ��99��A�������ܼ�+B�������ܼۡ�105����3������������ͬ��˵���������δ֪���أ���δ֪��x��ϵ��Ϊ0���ɣ����B�������Թ�˾����������ΪA������ÿ������Ϊ7.5��Ԫ��B������ÿ������Ϊ6��Ԫ������Ҫ���B�
�����㾫�����������⣬������Ҫ�˽��ʽ���̵�Ӧ��(�з�ʽ���̽�Ӧ����IJ��裺���⡢��δ֪��������ȹ�ϵ�з��̡��ⷽ�̲������д���𰸣�Ҫ�е�λ��)����Ҫ����һԪһ�β���ʽ���Ӧ��(1���������⣬�ҳ����ȹ�ϵ��2���裺��δ֪����3���У��г�����ʽ�飻4���⣺�ⲻ��ʽ�飻5�����飺�Ӳ���ʽ��Ľ⼯���ҳ���������Ĵ𰸣�6����д�������)�����֪ʶ���Ǵ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����ⱳ������֪����ͼ1��������ABC�У�AB=AC����BAC=120�㣬AD��BC�ڵ�D��AB=a����ABC�����ΪS������BC=![]() a��S=
a��S=![]() a2��
a2��
��2��Ǩ��Ӧ�ã���ͼ2����ABC����ADE���ǵ��������Σ���BAC=��DAE=120�㣬D��E��C������ͬһ��ֱ���ϣ�����BD��
����֤����ADB�ա�AEC��
������ADB�Ķ�����
����AD=2��BD=4������ABC�������
��3����չ���죺��ͼ3���ڵ�����ABC�У���BAC=120��������BAC��������AM����D���B��������AM��Գƣ�����CD���ӳ���AM�ڵ�E��AF��CD��F������AD��BE��
������EAF�Ķ�����
����CD=5��BD=2����BC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=��x+2��ͼ���뷴��������y=�� ![]() ��ͼ����A��B���㣬��x�ύ��D�㣬��C��D�������y��Գƣ�
��ͼ����A��B���㣬��x�ύ��D�㣬��C��D�������y��Գƣ� 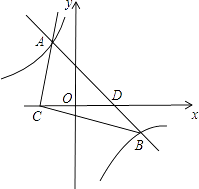
��1����A��B��������ꣻ
��2�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͨ���Կα��С�Ӳ�ҹ����е���ѧ����ѧϰ������֪������Բ����������ȡ���ڹ���Բ��Բ���˶���·�̣���ͼ�٣�����ͼ���У���2014���뾶Ϊr��Բ�������г�һ��ֱ�ߣ��뾶Ϊr�Ķ�ԲC��ͼʾλ������2014��Բ�ųɵ�ͼ�������ع���һȦ�ص�ԭλ����ԲC����ת��������Ϊ �� 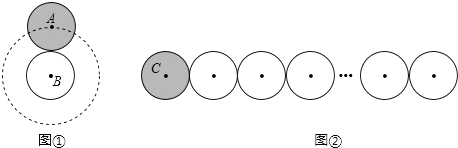
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��װ�깺��һ���ס������ֿ���ʱ��T���������ֿ�������7800Ԫ�����ֿ�������6400Ԫ�����ֿ��͵ļ��������ֿ��ͼ�����1.5�������ֿ���ÿ���Ľ��۱����ֿ���ÿ���Ľ�����30Ԫ��
��1���ס������ֿ��͵�T�������������ټ���
��2���̵�������60%������ۣ�����һ��ʱ�����ȫ�����꣬�ҿ���ʣ��һ�룬�̵�������ҿ��Ͱ���۵����۽������ۣ��ܿ�ȫ�����꣬������ ����T�����̵깲��������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ABCD�У�![]() ��
��![]() ��
��![]() ������BD������BDC�ǵȱ������Σ���ô����ABCD�������_________��
������BD������BDC�ǵȱ������Σ���ô����ABCD�������_________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
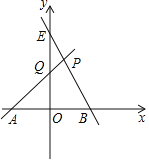
����Ŀ����ͼ����ֱ֪��AQ��x�Ḻ���ύ�ڵ�A����y�������ύ�ڵ�Q����QAO=45����ֱ��AQ��y���ϵĽؾ�Ϊ2��ֱ��BE��y=-2x+8��ֱ��AQ���ڵ�P��
��1����ֱ��AQ�Ľ���ʽ��
��2����y����������ȡһ��F�����ı���BPFO������ʱ�����F�����꣮
��3������C��y�Ḻ�����ϣ���M��ֱ��PA�ϣ���N��ֱ��PB�ϣ��Ƿ������Q��C��M��NΪ������ı��������Σ��������������C�����ꣻ����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
�У�![]() ��D��E��F�ֱ�ΪAB��BC��CA�ϵĵ㣬��
��D��E��F�ֱ�ΪAB��BC��CA�ϵĵ㣬��![]() ��
��![]() ��
��
��1����֤��![]() ��
��![]() ��
��
��2����![]() ����
����![]() �Ķ�����
�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AD=2AB��E��AD����һ�㣬DE= ![]() AD��nΪ����2��������������BE����BE�Ĵ�ֱƽ���߷ֱ�AD��BC�ڵ�F��G��FG��BE�Ľ���ΪO������BF��EG��
AD��nΪ����2��������������BE����BE�Ĵ�ֱƽ���߷ֱ�AD��BC�ڵ�F��G��FG��BE�Ľ���ΪO������BF��EG��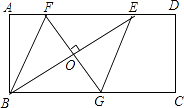
��1�����ж��ı���BFEG����״����˵�����ɣ�
��2����AB=a��aΪ��������n=3ʱ����FG�ij���
��3�����ı���BFEG�����ΪS1 �� ����ABCD�����ΪS2 �� �� ![]() =
= ![]() ʱ����n��ֵ����ֱ��д�����������д�������̣�
ʱ����n��ֵ����ֱ��д�����������д�������̣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com