练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

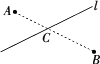
    如图，已知直线l是一条平直的公路，A、B是某公司的两个仓库，位于公路两旁，要在公路上建一货物中转站C，使A、B到C的距离之和最小，请找出点C的位置并说明理由．

    答案：
    解析：

    　　解：如题图，连结AB，与直线l的交点即为所找的点C．

    　　理由：根据“两点之间，线段最短”，要使A、B到C的距离之和最小，则点C必须在线段AB上．

    　　又因为点C必在直线l上，所以点C应是两线的交点．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，已知直线y=-x+b与双曲线y=
    bx
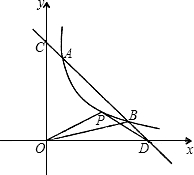    在第一象限内的一支相交于点A、B，与坐精英家教网标轴交于点C、D，P是双曲线上一点，PO=PD．
    （1）试用k、b表示点P的坐标；
    （2）若△POD的面积等于1，
    ①求双曲线在第一象限内的解析式；
    ②已知点A的纵坐标和点B的横坐标都是2，求△OAB的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2011•兰州一模）如图，已知直线AB是⊙O的切线，A为切点，OB交⊙O于点C，点D在⊙O上，且BC=CO，则tan∠ADC=
    		3
    3
    		3
    3
    ．

    查看答案和解析>>

    科目：初中数学 来源：数学教研室 题型：013

    给出以下两个定理：

    (1)线段垂直平分线上的点到这条线段两个端点的距离相等．

    (2)到一条线段两个端点距离相等的点，在这条线段的垂直平分线上．应用上述定理进行如下推理，如图，已知直线l是线段MN的垂直平分线．

    ∵点A在直线l上，∴AM=AN(　　)．

    ∵BM=BN，∴点B在直线l上(　　)．

    ∵CM≠CN，∴点C不在直线l上(　　)．

    以上推理中，各括号内应注明的理由依次是

    [　　]

    A．(2)(1)(1)
    B．(2)(1)(2)
    C．(1)(2)(2)
    D．(1)(2)(1)

    查看答案和解析>>

    科目：初中数学 来源： 题型：013

    给出以下两个定理：

    (1)线段垂直平分线上的点到这条线段两个端点的距离相等．

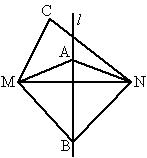
    (2)到一条线段两个端点距离相等的点，在这条线段的垂直平分线上．应用上述定理进行如下推理，如图，已知直线l是线段MN的垂直平分线．

    ∵点A在直线l上，∴AM=AN(　　)．

    ∵BM=BN，∴点B在直线l上(　　)．

    ∵CM≠CN，∴点C不在直线l上(　　)．

    以上推理中，各括号内应注明的理由依次是

    [　　]

    A．(2)(1)(1)
    B．(2)(1)(2)
    C．(1)(2)(2)
    D．(1)(2)(1)

    查看答案和解析>>

    同步练习册答案