
【题目】 今年“五一”假期,某教学活动小组组织一次登山活动,他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达山顶C点,路线如图所示,斜坡AB的长为200![]() 米,斜坡BC的长为200
米,斜坡BC的长为200![]() 米,坡度是1:1,已知A点海拔121米,C点海拔721米
米,坡度是1:1,已知A点海拔121米,C点海拔721米
(1)求B点的海拔;
(2)求斜坡AB的坡度;
(3)为了方便上下山,若在A到C之间架设一条钢缆,求钢缆AC的长度.
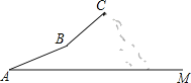
【答案】(1)521米;(2)2:3;(3)1000米.
【解析】
(1)根据题意和图形,可以求得点B的海拔;
(2)根据题目中的数据可以求得AF和BF的长度,从而可以求得斜坡AB的坡度;
(3)根据题目中的数据可以求得AD和CD的长度,然后根据勾股定理即可求得AC的长.
(1)如图,作CD⊥AM于点D,作BE⊥CD于点E,作BF⊥AM于点F,连接AC,

∵斜坡BC的长为200![]() 米,坡度是1:1,
米,坡度是1:1,
∴BE=CE=200米,
∵A点海拔121米,C点海拔721米,
∴CD=600米,
∴BF=400米,
∵121+400=521(米),
∴点B的海拔是521米;
(2)∵斜坡AB的长为200![]() 米,BF=400米,
米,BF=400米,
∴AF=![]() =600米,
=600米,
∴BF:AF=400:600=2:3,
即斜坡AB的坡度是2:3;
(3)∵CD=600米,AD=AF+FD=AF+BE=600+200=800(米),
∴AC=![]() =1000米,
=1000米,
即钢缆AC的长度是1000米.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.
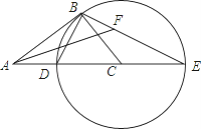
(1)求证:△ABD∽△AEB;
(2)当 ![]() =
= ![]() 时,求tanE;
时,求tanE;
(3)在(2)的条件下,作∠BAC的平分线,与BE交于点F,若AF=2,求⊙C的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组数据7,2,5,4,2的方差为a,若再增加一个数据4,这6个数据的方差为b,则a与b的大小关系是( )
A. a>b B. a=b C. a<b D. 以上都有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
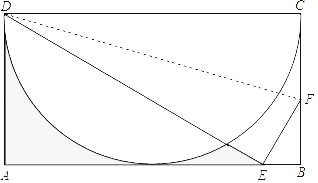
【题目】如图所示,ABCD为矩形,以CD为直径作半圆,矩形的另外三边分别与半圆相切,沿着折痕DF折叠该矩形,使得点C的对应点E落在AB边上,若AD=2,则图中阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
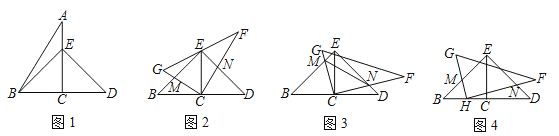
【题目】一副三角板如图1所置,其中AC边与等腰Rt△EBD斜边上的中线EC共线,以C点为旋转中心,顺时针转动△ACB,B、A两点分别于G、F两点对应,CG交BE边于点M,CF交DE边于N,已知旋转角为α,BC=2.
(问题发现)(1)如图2所示,若旋转角α(0°<α<30°)时,猜想CM与CN的数量关系,并写出你的推断过程;
(类比探究)(2)如图3所示,若旋转角α=75°时,(1)中的结论是否还成立? ,此时连接MN,请直接写出MN的长度为 ;
(拓展延伸)(3)在图3的基础上将△GCF向左平移至△GHF的位置,若DH=kBH,猜想线段HN与HM的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
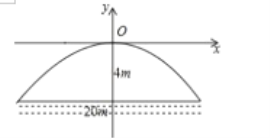
【题目】有一座抛物线形拱桥,正常水位桥下面宽度为![]() 米,拱顶距离水平面
米,拱顶距离水平面![]() 米,如图建立直角坐标系,若正常水位时,桥下水深
米,如图建立直角坐标系,若正常水位时,桥下水深![]() 米,为保证过往船只顺利航行,桥下水面宽度不得小于
米,为保证过往船只顺利航行,桥下水面宽度不得小于![]() 米,则当水深超过多少米时,就会影响过往船只的顺利航行( )
米,则当水深超过多少米时,就会影响过往船只的顺利航行( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
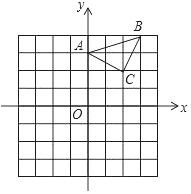
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度).
(1)作出△ABC绕点A顺时针方向旋转90°后得到的△A1B1C1,并直接写出C1点的坐标;
(2)作出△ABC关于原点O成中心对称的△A2B2C2,并直接写出B2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
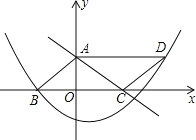
【题目】如图,点A、C分别是一次函数y=﹣![]() x+3的图象与y轴、x轴的交点,点B与点C关于原点对称,二次函数y=
x+3的图象与y轴、x轴的交点,点B与点C关于原点对称,二次函数y=![]() x2+bx+c的图象经过点B,且该二次函数图象上存在一点D,使四边形ABCD能构成平行四边形.
x2+bx+c的图象经过点B,且该二次函数图象上存在一点D,使四边形ABCD能构成平行四边形.
(1)求二次函数的表达式;
(2)动点P从点A到点D,同时动点Q从点C到点A都以每秒1个单位的速度运动,设运动时间为t秒.
①当t为何值时,有PQ丄AC?
②当t为何值时,四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
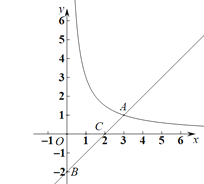
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图像与直线
的图像与直线![]() 交于点
交于点![]() ,直线
,直线![]() 分别交x轴,y轴于C、B两点.
分别交x轴,y轴于C、B两点.
(1)求![]() 的值;
的值;
(2)已知点![]() ,当点P在函数
,当点P在函数![]() 的图像上时,求△POA的面积;
的图像上时,求△POA的面积;
(3)点Q在函数![]() 的图像上滑动,现有以Q点为圆心,
的图像上滑动,现有以Q点为圆心,![]() 为半径的⊙Q,当⊙Q与直线
为半径的⊙Q,当⊙Q与直线![]() 相切时,求点Q的坐标.
相切时,求点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com