
分析 (1)根据两点间的距离公式,可得答案;
(2)根据两点间的距离公式,点在线段上,可得最小值;
(3):|x-3|+|x-2|+|x+1|=(|x-3|+|x+1|)+|x-2|,根据问题(2)中的探究②可知,要使|x-3|+|x+1|的值最小,x的值只要取-1到3之间(包括-1、3)的任意一个数,要使|x-2|的值最小,x应取2,显然当x=2时能同时满足要求,把x=2代入原式计算即可;
(4)根据两点间的距离公式,点在线段上,可得答案.
解答 解:(1)A到B的距离与A到C的距离之和可表示为|x+2|+|x-1|;
(2)①满足|x-3|+|x+1|=6的x的所有值是-2、4,
②这个最小值是4;当x的值取在不小于0且不大于2的范围时,|x|+|x-2|取得最小值,这个最小值是2;
(3)由分析可知,
当x=2时能同时满足要求,把x=2代入原式=1+0+3=4;
(4)|x-3|+|x-2|+|x+1|+|x+2|=(|x-3|+|x+2|)+(|x-2|+|x+1|)
要使|x-3|+|x+2|的值最小,x的值取-2到3之间(包括-2、3)的任意一个数,要使|x-2|+|x+1|的值最小,x取-1到2之间(包括-1、2)的任意一个数,显然当x取-1到2之间(包括-1、2)的任意一个数能同时满足要求,不妨取x=0代入原式,得|x-3|+|x-2|+|x+1|+|x+2|=3+2+1+2=8;
方法二:当x取在-1到2之间(包括-1、2)时,|x-3|+|x-2|+|x+1|+|x+2|=-(x-3)-(x-2)+(x+1)+(x+2)=-x+3-x+2+x+1+x+2=8.
故答案为:|x+2|+|x-1|;-2,4;4;不小于0且不大于2;2;4,2.
点评 本题考查了绝对值,读懂题目信息,理解绝对值的几何意义是解题的关键.


科目:初中数学 来源: 题型:解答题
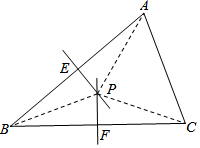 证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 按下列要求画图,并解答下列问题:
按下列要求画图,并解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com