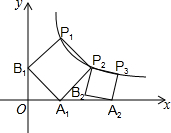
如图,正方形A
1B
1P
1P
2的顶点P
1、P
2在反比例函数y=
(x>0)的图象上,顶点A
1、B
1分别在x轴和y轴的正半轴上,再在其右侧作正方形P
2P
3A
2B
2,顶点P
3在反比例函数y=
(x>0)的图象上,顶点A
2在x轴的正半轴上,则P
2点的坐标为
(2,1)
(2,1)
,P
3的坐标为
.
分析:作P
1C⊥y轴于C,P
2D⊥x轴于D,P
3E⊥x轴于E,P
3F⊥P
2D于F,设P
1(a,
),则CP
1=a,OC=
,易得Rt△P
1B
1C≌Rt△B
1A
1O≌Rt△A
1P
2D,则OB
1=P
1C=A
1D=a,所以OA
1=B
1C=P
2D=
-a,则P
2的坐标为(
,
-a),然后把P
2的坐标代入反比例函数y=
,得到a的方程,解方程求出a,得到P
2的坐标;设P
3的坐标为(b,
),易得Rt△P
2P
3F≌Rt△A
2P
3E,则P
3E=P
3F=DE=
,通过OE=OD+DE=2+
=b,这样得到关于b的方程,解方程求出b,得到P
3的坐标.
解答: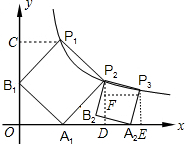
解:作P
1C⊥y轴于C,P
2D⊥x轴于D,P
3E⊥x轴于E,P
3F⊥P
2D于F,如图,
设P
1(a,
),则CP
1=a,OC=
,
∵四边形A
1B
1P
1P
2为正方形,
∴Rt△P
1B
1C≌Rt△B
1A
1O≌Rt△A
1P
2D,
∴OB
1=P
1C=A
1D=a,
∴OA
1=B
1C=P
2D=
-a,
∴OD=a+
-a=
,
∴P
2的坐标为(
,
-a),
把P
2的坐标代入y=
(x>0),得到(
-a)•
=2,解得a=-1(舍)或a=1,
∴P
2(2,1),
设P
3的坐标为(b,
),
又∵四边形P
2P
3A
2B
2为正方形,
∴P
2P
3=P
3A
2,∠P
3EA
2=∠P
2FP
3,
∴Rt△P
2P
3F≌Rt△A
2P
3E,
∴P
3E=P
3F=DE=
,
∴OE=OD+DE=2+
,
∴2+
=b,解得b=1-
(舍),b=1+
,
∴
=
=
-1,
∴点P
3的坐标为 (
+1,
-1).
故答案为:(2,1),(
+1,
-1).
点评:本题考查了反比例函数图象上点的坐标特点为横纵坐标之积为定值;也考查了正方形的性质和三角形全等的判定与性质以及解分式方程的方法.
练习册系列答案
相关习题
科目:初中数学
来源:
题型:
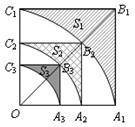
如图,正方形OA
1B
1C
1的边长为2,以O为圆心、OA
1为半径作弧A
1C
1交OB
1于点B
2,设弧A
1C
1与边A
1B
1、B
1C
1围成的阴影部分面积S
1;然后以OB
2为对角线作正方形OA
2B
2C
2,又以O为圆心、OA
2为半径作弧A
2C
2交OB
2于点B
3,设弧A
2C
2与边A
2B
2、B
2C
2围成的阴影部分面积为S
2;…,按此规律继续作下去,设弧A
nC
n与边A
nB
n、B
nC
n围成的阴影部分面积为S
a.则S
1=
,S
2=
,…,S
n=
.
查看答案和解析>>
科目:初中数学
来源:2011-2012学年辽宁省盘锦市四完中九年级(上)第四次月考数学试卷(解析版)
题型:填空题
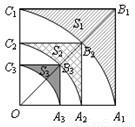
如图,正方形OA
1B
1C
1的边长为2,以O为圆心、OA
1为半径作弧A
1C
1交OB
1于点B
2,设弧A
1C
1与边A
1B
1、B
1C
1围成的阴影部分面积S
1;然后以OB
2为对角线作正方形OA
2B
2C
2,又以O为圆心、OA
2为半径作弧A
2C
2交OB
2于点B
3,设弧A
2C
2与边A
2B
2、B
2C
2围成的阴影部分面积为S
2;…,按此规律继续作下去,设弧A
nC
n与边A
nB
n、B
nC
n围成的阴影部分面积为S
a.则S
1=
,S
2=
,…,S
n=
.

查看答案和解析>>
科目:初中数学
来源:2009-2010学年浙江省丽水市莲都区九年级(上)第三次月考数学试卷(解析版)
题型:填空题
如图,正方形OA
1B
1C
1的边长为2,以O为圆心、OA
1为半径作弧A
1C
1交OB
1于点B
2,设弧A
1C
1与边A
1B
1、B
1C
1围成的阴影部分面积S
1;然后以OB
2为对角线作正方形OA
2B
2C
2,又以O为圆心、OA
2为半径作弧A
2C
2交OB
2于点B
3,设弧A
2C
2与边A
2B
2、B
2C
2围成的阴影部分面积为S
2;…,按此规律继续作下去,设弧A
nC
n与边A
nB
n、B
nC
n围成的阴影部分面积为S
a.则S
1=
,S
2=
,…,S
n=
.
查看答案和解析>>
科目:初中数学
来源:2010年北京市东城区中考数学二模试卷(解析版)
题型:填空题
如图,正方形OA
1B
1C
1的边长为2,以O为圆心、OA
1为半径作弧A
1C
1交OB
1于点B
2,设弧A
1C
1与边A
1B
1、B
1C
1围成的阴影部分面积S
1;然后以OB
2为对角线作正方形OA
2B
2C
2,又以O为圆心、OA
2为半径作弧A
2C
2交OB
2于点B
3,设弧A
2C
2与边A
2B
2、B
2C
2围成的阴影部分面积为S
2;…,按此规律继续作下去,设弧A
nC
n与边A
nB
n、B
nC
n围成的阴影部分面积为S
a.则S
1=
,S
2=
,…,S
n=
.
查看答案和解析>>
科目:初中数学
来源:2010年浙江省杭州市萧山区中考数学模拟试卷47(河庄镇中 陈国亚)(解析版)
题型:填空题
(2010•东城区二模)如图,正方形OA
1B
1C
1的边长为2,以O为圆心、OA
1为半径作弧A
1C
1交OB
1于点B
2,设弧A
1C
1与边A
1B
1、B
1C
1围成的阴影部分面积S
1;然后以OB
2为对角线作正方形OA
2B
2C
2,又以O为圆心、OA
2为半径作弧A
2C
2交OB
2于点B
3,设弧A
2C
2与边A
2B
2、B
2C
2围成的阴影部分面积为S
2;…,按此规律继续作下去,设弧A
nC
n与边A
nB
n、B
nC
n围成的阴影部分面积为S
a.则S
1=
,S
2=
,…,S
n=
.

查看答案和解析>>

 如图,正方形A1B1P1P2的顶点P1、P2在反比例函数y=
如图,正方形A1B1P1P2的顶点P1、P2在反比例函数y= 解:作P1C⊥y轴于C,P2D⊥x轴于D,P3E⊥x轴于E,P3F⊥P2D于F,如图,
解:作P1C⊥y轴于C,P2D⊥x轴于D,P3E⊥x轴于E,P3F⊥P2D于F,如图,

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案 如图,正方形OA1B1C1的边长为2,以O为圆心、OA1为半径作弧A1C1交OB1于点B2,设弧A1C1与边A1B1、B1C1围成的阴影部分面积S1;然后以OB2为对角线作正方形OA2B2C2,又以O为圆心、OA2为半径作弧A2C2交OB2于点B3,设弧A2C2与边A2B2、B2C2围成的阴影部分面积为S2;…,按此规律继续作下去,设弧AnCn与边AnBn、BnCn围成的阴影部分面积为Sa.则S1=
如图,正方形OA1B1C1的边长为2,以O为圆心、OA1为半径作弧A1C1交OB1于点B2,设弧A1C1与边A1B1、B1C1围成的阴影部分面积S1;然后以OB2为对角线作正方形OA2B2C2,又以O为圆心、OA2为半径作弧A2C2交OB2于点B3,设弧A2C2与边A2B2、B2C2围成的阴影部分面积为S2;…,按此规律继续作下去,设弧AnCn与边AnBn、BnCn围成的阴影部分面积为Sa.则S1=


