
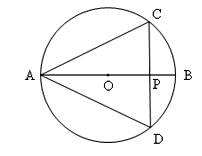
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若AB=2,AC=![]() .
.
(1)求∠A的度数.
(2)求弧CBD的长.
(3)求弓形CBD的面积.
【答案】(1)∠A=30°;(2)![]() ;(3)
;(3)![]() -
-![]() .
.
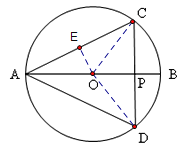
【解析】试题分析:(1)过O作OE⊥AC,由垂径定理可得AE的长,再用三角函数即可求得∠A的度数;
(2)由∠A得度数得出对应圆心角∠COB的度数,由垂径定理得∠DOB=∠COB,由此得到∠COD的度数,用弧长公式即可求出弧长;
(3)由公式:弓形CBD的面积=扇形COD的面积△COD的面积,即可求出弓形面积.
试题解析:(1)过O作OE⊥AC,
![]() ,
,
![]()
在Rt△AEO中, ![]()
![]()
(2)连结OC,OD, ![]()
![]()
∵AB是⊙O的直径,弦CD⊥AB,
∴![]() =
=![]() ,
,
![]()
![]()
∵AB=2,
![]()
∴![]() 的长=
的长=![]() ;
;
(3) ![]() OP⊥CD,
OP⊥CD,
![]()
∵OC=1,
![]()
![]() ,
,
∴弓形CBD的面积=扇形COD的面积△COD的面积![]()


科目:初中数学 来源: 题型:
【题目】已知数轴上的A、B两点分别对应的数字为a、b,且a、b满足|4a-b|+(a-4)2=0.
(1)直接写出a、b的值;
(2)P从A出发,以每秒3个长度的速速延数轴正方向运动,当PA=PB时,求P运动的时间和P表示的数;
(3)数轴上还有一点C对应的数为36,若点P从A出发,以每秒3个单位的速度向C点运动,同时,Q从B点出发,以每秒1个长度的速度向正方向运动,点P运动到C点立立即返回再沿数轴向左运动.当PQ=10时,求P点对应的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是BC的中点,F是线段CD上的动点.
(1)如图1,若CF=![]() CD,求证:ΔAEF是直角三角形;
CD,求证:ΔAEF是直角三角形;
(2)如图2,若点F与点D重合,点G在ED上,且AG=AD,求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )

A. 14 B. 16 C. 17 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)有4张桌子,用第一种摆设方式,可以坐 人;用第二种摆设方式,可以坐 人;
(2)有n张桌子,用第一种摆设方式可以坐 人;用第二种摆设方式,可以坐 人(用含有n的代数式表示);
(3)一天中午,餐厅要接待120位顾客共同就餐,但餐厅中只有30张这样的长方形桌子可用,且每6张拼成一张大桌子,若你是这家餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
符号、p分别表示一种运算,它对一些数的运算结果如下:
(0)=-1, (1)=0 , (2)=1 , (-3)=-4, (-4)=-5,……
p(-1)=-2,p(![]() )=1,p(
)=1,p(![]() )=
)=![]() , p(2)=4, p(-3)=-6,……
, p(2)=4, p(-3)=-6,……
根据以上运算规律,完成下列问题:
(1)计算:(-5)×p(![]() )+2
)+2
(2)已知x为有理数,且(x)+ p(![]() )=2×(-4),求x的值。
)=2×(-4),求x的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,回答下列问题:
数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题。例如,两个有理数在数轴上对应的点之间的距离可以用这两个数的差的绝对值表示;
在数轴上,有理数3与1对应的两点之间的距离为|31|=2;
在数轴上,有理数5与2对应的两点之间的距离为|5(2)|=7;
在数轴上,有理数2与3对应的两点之间的距离为|23|=5;
在数轴上,有理数8与5对应的两点之间的距离为|8(5)|=3;……
如图1,在数轴上有理数a对应的点为点A,有理数b对应的点为点B,A,B两点之间的距离表示为|ab|或|ba|,记为|AB|=|ab|=|ba|.

(1)数轴上有理数10与5对应的两点之间的距离等于___;数轴上有理数x与5对应的两点之间的距离用含x的式子表示为___;若数轴上有理数x与1对应的两点A,B之间的距离|AB|=2,则x等于___;
(2)如图2,点M,N,P是数轴上的三点,点M表示的数为4,点N表示的数为2,动点P表示的数为x.

①若点P在点M,N之间,则|x+2|+|x4|=___;若|x+2|+|x4|═10,则x=___;
②根据阅读材料及上述各题的解答方法,|x+2|+|x|+|x2|+|x4|的最小值等于___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com