
 x2+bx+c��x���ڵ�A��m��0���͵�B����y���ڵ�C��0��m����
x2+bx+c��x���ڵ�A��m��0���͵�B����y���ڵ�C��0��m����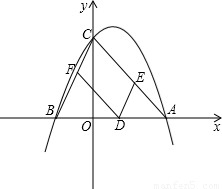
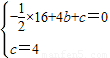 ��
��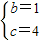 ��
�� x2+x+4��
x2+x+4�� AB•OC=12��
AB•OC=12��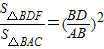 =
= ��
�� ��d+2��2��
��d+2��2�� ��4-d��2��
��4-d��2�� ��d+2��2-
��d+2��2- ��4-d��2
��4-d��2 d2+
d2+ d+
d+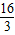 =-
=- ��d-1��2+6��
��d-1��2+6��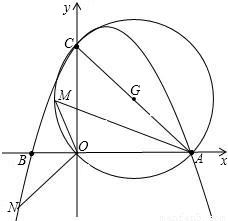 ����A��4��0����C��0��4������ôOA=OC=4������OAC�ǵ���ֱ�������Σ�
����A��4��0����C��0��4������ôOA=OC=4������OAC�ǵ���ֱ�������Σ� m2+m+4����ã�m=-2
m2+m+4����ã�m=-2 ����ֵ��ȥ����
����ֵ��ȥ���� ��-2
��-2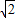 ����
����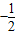 m2+m+4��
m2+m+4�� ����ֵ��ȥ����
����ֵ��ȥ���� ��2
��2 -2����
-2���� ��-2
��-2 ����2-2
����2-2 ��2
��2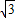 -2����
-2����


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
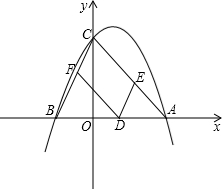 ��ͼ��ʾ����֪ʵ��m�Ƿ���x2-8x+16=0��һ��ʵ������������y=-
��ͼ��ʾ����֪ʵ��m�Ƿ���x2-8x+16=0��һ��ʵ������������y=-| 1 | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����2�¡����κ������п��⼯��35����2.8 ���κ�����Ӧ�ã������棩 ���ͣ������
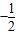 x2+bx+c��x���ڵ�A��m��0���͵�B����y���ڵ�C��0��m����
x2+bx+c��x���ڵ�A��m��0���͵�B����y���ڵ�C��0��m����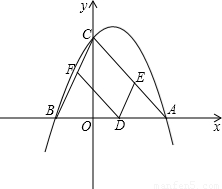
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����23�¡����κ����뷴�����������п��⼯��31����23.5 ���κ�����Ӧ�ã������棩 ���ͣ������
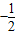 x2+bx+c��x���ڵ�A��m��0���͵�B����y���ڵ�C��0��m����
x2+bx+c��x���ڵ�A��m��0���͵�B����y���ڵ�C��0��m����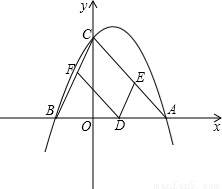
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013��ӱ�ʡ�п���ѧģ���Ծ���ʮ�����������棩 ���ͣ������
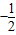 x2+bx+c��x���ڵ�A��m��0���͵�B����y���ڵ�C��0��m����
x2+bx+c��x���ڵ�A��m��0���͵�B����y���ڵ�C��0��m����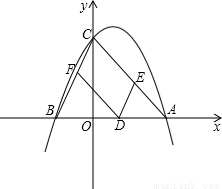
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012�����ɹŰ��������п���ѧ�Ծ����������������棩 ���ͣ������
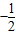 x2+bx+c��x���ڵ�A��m��0���͵�B����y���ڵ�C��0��m����
x2+bx+c��x���ڵ�A��m��0���͵�B����y���ڵ�C��0��m����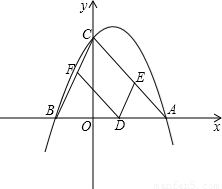
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com