
【题目】如图,抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC、CD. 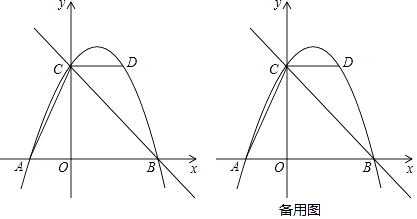
(1)求抛物线的函数表达式;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标.
【答案】
(1)解:∵抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),点D(2,4),
∴设抛物线的解析式为y=a(x﹣x1)(x﹣x2),
∴y=a(x+2)(x﹣4),
∴﹣8a=4,
∴a=﹣ ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() (x+2)(x﹣4)=﹣
(x+2)(x﹣4)=﹣ ![]() x2+x+4
x2+x+4
(2)解:①当点E在直线CD的抛物线上方,记E′,连接CE′,过点E′作E′F′⊥CD,垂足为F′,
由(1)得OC=4,
∵∠ACO=∠E′OF′,
∴tan∠ACO=tan∠E′CF′,
∴ ![]() =
= ![]() =
= ![]() ,
,
设线段E′F′=h,则CF′=2h,
∴点E′(2h,h+4),
∵点E′在抛物线上,
∴﹣ ![]() (2h)2+2h+4=h+4,
(2h)2+2h+4=h+4,
∴h1=0(舍去),h2= ![]() ,
,
∴E′(1, ![]() );
);
②当点E在直线CD的抛物线下方;
同①的方法得,E(3, ![]() ),
),
综上,点E的坐标为(1, ![]() ),(3,
),(3, ![]() ).
).
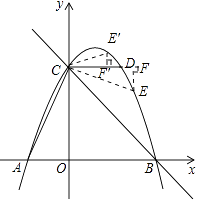
【解析】(1)设抛物线的解析式为y=a(x﹣x1)(x﹣x2),再把点代入即可得出解析式;(2)分两种情况:①当点E在直线CD的抛物线上方;②当点E在直线CD的抛物线下方;连接CE,过点E作EF⊥CD,再由三角函数得出点E的坐标.


科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1 . 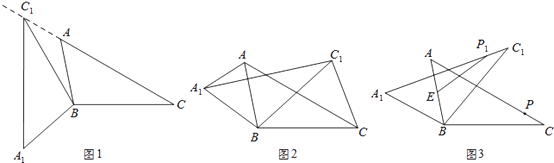
(1)如图1,当点C1在线段CA的延长线时,求∠CC1A1的度数;
(2)已知AB=6,BC=8,
①如图2,连接AA1 , CC1 , 若△CBC1的面积为16,求△ABA1的面积;
②如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转的过程中,点P的对应是点P1 , 直接写出线段EP1长度的最大值.
(3)线段EP1长度的最大值为11,理由如下:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是_______(只填写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在数轴上标出数﹣4.5,﹣2,1,3.5所对应的点A,B,C,D;
(2)C,D两点间距离=_____;B,C两点间距离=_____;
(3)数轴上有两点M,N,点M对应的数为a,点N对应的数为b,那么M,N两点之间的距离=_____;
(4)若动点P,Q分别从点B,C同时出发,沿数轴负方向运动;已知点P的速度是每秒1个单位长度,点Q的速度是每秒2个单位长度,问①t为何值时P,Q两点重合?②t为何值时P,Q两点之间的距离为1?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,∠A=36°,AC的垂直平分线MN交AB于D,AC于M,以下结论:
①△BCD是等腰三角形;②射线CD是∠ACB的角平分线;③△BCD的周长C△BCD=AB+BC;④△ADM≌△BCD。
正确的有( )

A. ①② B. ①③ C. ①②③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣37)﹣(﹣47) (2)10﹣(﹣5)+(﹣9)+6.
(3))-7+13-6+20 (4)0.125+3![]() -(+3
-(+3![]() )+(﹣0.25)
)+(﹣0.25)
(5)﹣|﹣1|+|![]() ﹣
﹣![]() |+(﹣2).
|+(﹣2).
(6)1+(﹣2)+3+(﹣4)+…+2017+(﹣2018)+2019+(﹣2020)
(7)(﹣5![]() )+(﹣9
)+(﹣9![]() )+17
)+17![]() +(﹣3
+(﹣3![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴子A、B两点,与反比例函数y![]() 的图象交于C、D两点,DE⊥x轴于点E,已知点C的坐标是(6,-1),DE=3.
的图象交于C、D两点,DE⊥x轴于点E,已知点C的坐标是(6,-1),DE=3.
(1)求反比例函数与一次函数的关系式;
(2)根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用:

(1)如图,可以求出阴影部分的面积是_____(写成两数平方差的形式);
(2)如图,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是_____,长是_____,面积是________(写成多项式乘法的形式);
(3)比较左、右两图的阴影部分面积,可以得到乘法公式:_________(用式子表达);
(4)运用你所得到的公式,计算下列式子:(2m+n﹣p)(2m﹣n+p)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com