
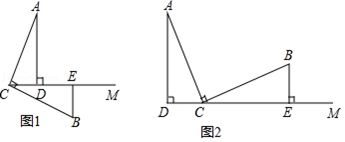
分析 (1)根据同角的余角相等,全等三角形的判定和性质即可解决问题;
(2)结论:DE-BE=AD,只要证明△ACD≌△CBE即可解决问题;
解答 解:(1)∵AD⊥CM,BE⊥CM,
∴∠ACB=∠BEC=∠ADC=90°,
∴∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE
在△ACD和△CBE中,( $\left\{\begin{array}{l}{∠ADC=∠BEC}\\{∠ACD=∠CBE}\\{AC=BC}\end{array}\right.$)
∴△ACD≌△CBE,( AAS)
∴CD=BE.
②结论:AD=BE+DE.
理由:∵△ACD≌△CBE,
∴AD=CE
∵CE=CD+DE=BE+DE,
∴AD=BE+DE.
故答案为:∠CBE,$\left\{\begin{array}{l}{∠ADC=∠BEC}\\{∠ACD=∠CBE}\\{AC=BC}\end{array}\right.$,AAS,AD=CE.
(2)不成立,结论:DE-BE=AD.
理由:∵AD⊥CM,BE⊥CM,
∴∠ACB=∠BEC=∠ADC=90°,
∴∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE
在△ACD和△CBE中,
$\left\{\begin{array}{l}{∠ADC=∠BEC}\\{∠ACD=∠CBE}\\{AC=BC}\end{array}\right.$,
∴△ACD≌△CBE,( AAS)
∴AD=CE,CD=BE,
∴DE-BE=DE-DC=CE=AD.
点评 本题考查全等三角形的判定和性质,解题的关键是正确寻找全等三角形的全等条件,灵活运用知识解决问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | 16 | C. | 20 | D. | 16或20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 周末小明从家出发沿金牛山公园散步,经过篮球场地看了一会篮球赛,然后继续散步了一段时间,最后回到家中,如图描述了小明散步过程中离家的距离s(米)与散步时间t(分)间的关系,下列说法错误的是( )
周末小明从家出发沿金牛山公园散步,经过篮球场地看了一会篮球赛,然后继续散步了一段时间,最后回到家中,如图描述了小明散步过程中离家的距离s(米)与散步时间t(分)间的关系,下列说法错误的是( )| A. | 小明看篮球赛用时16分钟 | B. | 篮球场地距小明家600米 | ||
| C. | 小明离家最远距离为1200米 | D. | 小明从家出发到回家共用时32分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 汽车行驶时间t(h) | 0 | 1 | 2 | 3 | … |
| 油箱剩余油量Q(L) | 100 | 94 | 88 | 82 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
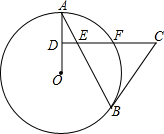 如图,CB是⊙O的切线,切点为B,CD⊥半径OA于D,交弦AB于点E,交⊙O于点F.
如图,CB是⊙O的切线,切点为B,CD⊥半径OA于D,交弦AB于点E,交⊙O于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com