解:(1)分两种情况:
①当DP⊥AC,DQ⊥BC时,
∵∠A=∠B,∠APD=∠BQD=90°,AD=BD,
∴△ADP≌△BDQ,∴DP=DQ;
②当DP、AC不垂直,DQ、BC不垂直时;
如图1,过D作DM⊥AC于M,DN⊥BC于N,由①可得DM=DN;
在四边形CMDN中,∠DMC=∠DNC=90°,∴∠MDN+∠MCN=180°;
又∵∠MCN+2∠A=180°,∴∠MDN=∠PDQ=2∠A=2α;
∴∠PDM=∠QDN=2α-∠MDQ,
又∵∠DMP=∠DNQ=90°,DM=DN,
∴△DMP≌△DNQ,得DP=DQ;
综合上面两种情况,得:当点P、Q分别在AC、BC上,且AD=BD时,DP、DQ的数量关系为:相等.

(2)图2、图3的结论与图1的完全相同,证法一致;以图2为例进行说明:
图2中,过D作DM⊥AC于M,DN⊥BC于N,则DM=DN;
同(1)可得:∠MDN=∠PDQ=2α,则∠PDM=∠QDN=2α-∠PDN,
又∵∠DMP=∠DNQ=90°,DM=DN,
∴△DMP≌△DNQ,得DP=DQ;
图3的证法同上;
所以在图2、图3中,(1)的结论依然成立,即DP、DQ的数量关系为:相等.
(3)DP、DQ的数量关系为:DP=nDQ,理由如下:
如图4,过D作DM⊥AC于M,DN⊥BC于N;
∵∠A=∠B,∠AMD=∠BND=90°,
∴△ADM∽△BDN,
∴

,即AD=nBD;

同上可得:∠MDN=∠PDQ=2∠A=2α;
∴∠MDP=∠NDQ=2α+∠NDP,
又∵∠DMP=∠DNQ=90°,
∴△DMP∽△DNQ,得:

,即DP=nDQ;
所以在(3)题的条件下,DP、DQ的数量关系为:DP=nDQ.
分析:(1)此题应分两种情况讨论,
①DP⊥AC,DQ⊥BC,显然此时△ADP≌△BDQ,得DP=DQ;
②DP、AC不垂直,DQ、BC不垂直,那么需要通过构造全等三角形来求解;仿照①的思路,可过D作AC、BC的垂线,设垂足为M、N,由①知DM=DN,然后通过证△DMP≌△DNQ来得到DP=DQ的结论.
(2)图2、图3的证法与(1)②的思路完全一样,都需要过D作AC、BC的垂线,通过构造的全等三角形来得到DP、DQ的数量关系.
(3)此题依然要沿用前面两问的思路;过D作AC、BC的垂线,DM、DN;然后通过两步相似来求解,首先通过△ADM∽△BDN来得到DM、DN的比例关系,然后通过△DMP∽△DNQ来得到DP、DQ的数量关系.
点评:此题主要考查的是全等三角形及相似三角形的判定和性质,正确地构造出与已知和所求相关的全等或相似三角形,是解答此题的关键.

 ∠PDQ=α.
∠PDQ=α.
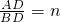 ,作∠PDQ=2a,使点P在AC上,点Q在BC的延长线上,完成图4,判断DP与DQ的数量关系,证明你的结论.
,作∠PDQ=2a,使点P在AC上,点Q在BC的延长线上,完成图4,判断DP与DQ的数量关系,证明你的结论.
 ,即AD=nBD;
,即AD=nBD;
 ,即DP=nDQ;
,即DP=nDQ;
