练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．如图，将三角形纸板ABC沿直线AB向右平行移动，使∠CAB到达∠DBE的位置，若∠CAB=50°，∠ABC=100°，则∠CBE的度数为（　　）
    A．50°B．40°C．30°D．100°

    分析 根据平移的性质得出AC∥BE，以及∠CAB=∠EBD=50°，进而求出∠CBE的度数．

    解答 解：∵将△ABC沿直线AB向右平移后到达△BDE的位置，
    ∴AC∥BE，
    ∴∠CAB=∠EBD=50°，
    ∵∠ABC=100°，
    ∴∠CBE的度数为：180°-50°-100°=30°．
    故选C．

    点评 此题主要考查了平移的性质以及三角形内角和定理，得出∠CAB=∠EBD=50°是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    20．下列调查中，最适宜采用全面调查方式的是（　　）
    A．对广水市中学生每天学习所用时间的调查
    B．对全国中学生心理健康现状的调查
    C．对某班学生进行6月5日是“世界环境日”知晓情况的调查
    D．对广水市初中学生视力情况的调查

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．将直线y=-x+2向下平移3个单位，所得直线经过的象限是二、三、四．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．已知方程组$\left\{\begin{array}{l}{ax+5y=15（1）}\\{4x-by=-2（2）}\end{array}\right.$，由于甲看错了方程（1）中的 a 得到方程组的解为$\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$，乙看错了方程（2）中的 b 得到方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$．若按正确的 a、b 计算，求原方程组的解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

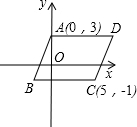    5．如图所示，在平面直角坐标系中，AD∥BC∥x轴，AD=BC=7，A（0，3），C（5，-1）．
    （1）求B、D两点坐标；
    （2）求四边形ABCD面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如图，在△ABC中，AB=AC，∠BAC=108°，AD、AE将∠BAC三等分交边BC于点D，点E，则下列结论中错误的是（　　）
    A．$\frac{BD}{DE}$=$\frac{\sqrt{5}-1}{2}$B．点D是线段BC的黄金分割点
    C．点E是线段BC的黄金分割点D．点E是线段CD的黄金分割点

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．某商店准备进一批季节性小家电，单价40元．经市场预测，销售定价为52元时，可售出180个，定价每增加1元，销售量净减少10个；定价每减少1元，销售量净增加10个．商店若准备获利2000元，则应进货多少个？定价为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．为了备战2016年里约奥运会，中国射击队正在积极训练．甲、乙两名运动员在相同的条件下，各射击10次．经过计算，甲、乙两人成绩的平均数均是9.5环，甲的成绩方差是0.125，乙的成绩的方差是0.85，那么这10次射击中，甲、乙成绩的稳定情况是（　　）
    A．甲较为稳定B．乙较为稳定
    C．两个人成绩一样稳定D．不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．有这样一个问题：如图，在四边形ABCD中，AB=AD，CB=CD，我们把这种两组邻边分别相等的四边形叫做筝形．请探究筝形的性质与判定方法．
    小南根据学习四边形的经验，对筝形的性质和判定方法进行了探究．
    下面是小南的探究过程：
    （1）由筝形的定义可知，筝形的边的性质是：筝形的两组邻边分别相等，关于筝形的角的性质，通过测量，折纸的方法，猜想：筝形有一组对角相等，请将下面证明此猜想的过程补充完整；
    已知：如图，在筝形ABCD中，AB=AD，CB=CD．
    求证：∠B=∠D．
    证明：连接AC，
    在△ABC和△ADC中，
    $\left\{\begin{array}{l}\;AB=AD\\ \;BC=DC\\ AC=AC\end{array}\right.$，
    ∴△ABC≌△ADC（SSS），
    ∴∠B=∠D
    由以上证明可得，筝形的角的性质是：筝形有一组对角相等．
    （2）连接筝形的两条对角线，探究发现筝形的另一条性质：筝形的一条对角线平分另一条对角线．结合图形，写出筝形的其他性质（一条即可）：筝形的两条对角线互相垂直．
    （3）筝形的定义是判定一个四边形为筝形的方法之一．从边、角、对角线或性质的逆命题等角度可以进一步探究筝形的判定方法，请你写出筝形的一个判定方法（定义除外），并说明你的结论．

    查看答案和解析>>

    同步练习册答案