
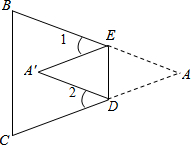
 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,分析 (1)根据翻折方法可得△ADE≌△A′DE;
(2)根据翻折方法可得∠AEA′=2x°,∠ADA′=2y°,再根据平角定义可得∠1=(180-2x)°,∠2=(180-2y)°;
(3)首先由∠1=(180-2x)°,∠2=(180-2y)°,可得x=90-$\frac{1}{2}∠1$,y=90-$\frac{1}{2}∠2$,再根据三角形内角和定理可得∠A=180°-x-y,再利用等量代换可得∠A=$\frac{1}{2}$(∠1+∠2).
解答 解:(1)△ADE≌△A′DE;
(2)∵∠AED=x°,∠ADE=y°,
∴∠AEA′=2x°,∠ADA′=2y°,
∴∠1=(180-2x)°,
∠2=(180-2y)°;
(3)∠A=$\frac{1}{2}$(∠1+∠2);
∵∠1=(180-2x)°①,
∠2=(180-2y)°②,
∴x=90-$\frac{1}{2}∠1$,y=90-$\frac{1}{2}∠2$,
∴∠A=180°-x-y=190-(90-$\frac{1}{2}$∠1)-(90-$\frac{1}{2}∠2$)=$\frac{1}{2}$(∠1+∠2).
点评 此题主要考查了翻折变换,关键是掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\frac{3}{4}$,0) | B. | (0,-3) | C. | (0,3) | D. | (0,$\frac{3}{4}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
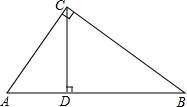 如图,△ABC为直角三角形,∠ACB=90°,CD为斜边AB上的高,D为垂足,△ABC∽△ACD∽△CBD,那么下列等式:①AC2=AD•AB;②CD2=AD•BD;③BC2=BD•AB;④AC•CB=BA•CD,其中正确的有①②③④.(填序号)
如图,△ABC为直角三角形,∠ACB=90°,CD为斜边AB上的高,D为垂足,△ABC∽△ACD∽△CBD,那么下列等式:①AC2=AD•AB;②CD2=AD•BD;③BC2=BD•AB;④AC•CB=BA•CD,其中正确的有①②③④.(填序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com