
【题目】二次函数y=ax2+bx+c图象如图,下列正确的个数为( )
①bc>0;
②2a﹣3c<0;
③2a+b>0;
④ax2+bx+c=0有两个解x1 , x2 , 当x1>x2时,x1>0,x2<0;
⑤a+b+c>0;
⑥当x>1时,y随x增大而减小.
A.2
B.3
C.4
D.5
【答案】B
【解析】解:①∵抛物线开口向上,
∴a>0,
∵对称轴在y轴右侧,
∴a,b异号即b<0,
∵抛物线与y轴的交点在负半轴,
∴c<0,
∴bc>0,故①正确;
②∵a>0,c<0,
∴2a﹣3c>0,故②错误;
③∵对称轴x=﹣ ![]() <1,a>0,
<1,a>0,
∴﹣b<2a,
∴2a+b>0,故③正确;
④由图形可知二次函数y=ax2+bx+c与x轴的两个交点分别在原点的左右两侧,
即方程ax2+bx+c=0有两个解x1 , x2 , 当x1>x2时,x1>0,x2<0,故④正确;
⑤由图形可知x=1时,y=a+b+c<0,故⑤错误;
⑥∵a>0,对称轴x=1,
∴当x>1时,y随x增大而增大,故⑥错误.
综上所述,正确的结论是①③④,共3个.
故选:B.
【考点精析】关于本题考查的二次函数图象以及系数a、b、c的关系,需要了解二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】已知:如图,Rt△ABC中,∠ABC=90°,AD平分∠BAC交BC于D. 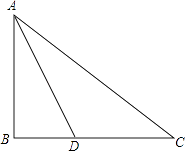
(1)用尺规画圆O,使圆O过A、D两点,且圆心O在边AC上.(保留作图痕迹,不写作法)
(2)求证:BC与圆O相切;
(3)设圆O交AB于点E,若AE=2,CD=2BD.求线段BE的长和弧DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),抛物线y=﹣ ![]() x2+x+c与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(﹣2,0).
x2+x+c与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(﹣2,0).
(1)求此抛物线的解析式;
(2)①若点D是第一象限内抛物线上的一个动点,过点D作DE⊥x轴于E,连接CD,以OE为直径作⊙M,如图(2),试求当CD与⊙M相切时D点的坐标;
②点F是x轴上的动点,在抛物线上是否存在一点G,使A、C、G、F四点为顶点的四边形是平行四边形?若存在,求出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、F分别是BC、CD的中点,DE交AF于点M,点N为DE的中点. 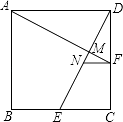
(1)若AB=4,求△DNF的周长及sin∠DAF的值;
(2)求证:2ADNF=DEDM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF、CE,且∠FBD=35°,∠BDF=75°,下列说法:①△BDF≌CDE;②ABD和△ACD面积相等;③BF∥CE;④∠DEC=70°,其中正确的有( )
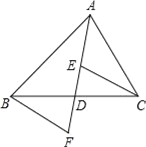
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD为等腰梯形,AD∥BC,AB=CD,AD= ![]() ,E为CD中点,连接AE,且AE=2
,E为CD中点,连接AE,且AE=2 ![]() ,∠DAE=30°,作AE⊥AF交BC于F,则BF=( )
,∠DAE=30°,作AE⊥AF交BC于F,则BF=( ) 
A.1
B.3﹣ ![]()
C.![]() ﹣1
﹣1
D.4﹣2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD. 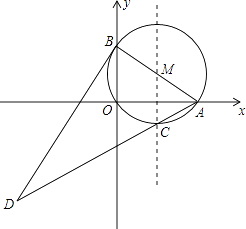
(1)求⊙M的半径;
(2)证明:BD为⊙M的切线;
(3)在直线MC上找一点P,使|DP﹣AP|最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com