
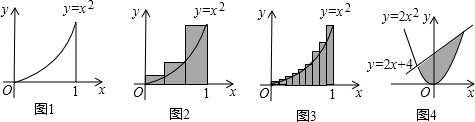
分析 (1)将n2=$\frac{n(n+1)(an+b)}{1•2•3}$-$\frac{(n-1)n[a(n-1)+b]}{1•2•3}$通分化简,根据恒等式的性质,列出方程即可解决问题.再模仿例题即可解决问题.
(2)①根据矩形的面积公式即可即可.
②根据矩形的面积公式以及(1)中的结论即可即可.
③由Sn=$\frac{1}{{n}^{3}}$(12+22+32+…+n2)=$\frac{n(n+1)(2n+1)}{6{n}^{3}}$=$\frac{2{n}^{3}+{3n}^{2}+n}{6{n}^{3}}$=$\frac{1}{3}$+$\frac{1}{2n}$+$\frac{1}{6{n}^{2}}$,因为n充分大时,$\frac{1}{2n}$、$\frac{1}{6{n}^{2}}$接近于0,所以Sn的值逼近于$\frac{1}{3}$.
(3)如图4中,设抛物线y=2x2与直线y=2x+4的交点为A、B,作AE⊥x轴于E,BF⊥x轴于F.记曲边三角形AEO的面积为S1,曲边三角形OBF的面积为S2.首先利用逼近法求出S1、S2,再根据S阴=S梯形AEFB-S1-S2计算即可.
解答 解:(1)∵n2=$\frac{n(n+1)(an+b)}{1•2•3}$-$\frac{(n-1)n[a(n-1)+b]}{1•2•3}$=$\frac{({n}^{2}+n)(an+b)-({n}^{2}-n)(an-a+b)}{6}$=$\frac{3a{n}^{2}-an+2bn}{1•2•3}$,
∴a=2,b=1时等式成立.
∴12+22+32+…+n2=$\frac{1•2•3}{1•2•3}$-$\frac{0}{1•2•3}$+$\frac{2•3•5}{1•2•3}$-$\frac{1•2•3}{1•2•3}$+…$\frac{n(n+1)(2n+1)}{1•2•3}$-$\frac{(n-1)n(2n-1)}{1•2•3}$=$\frac{n(n+1)(2n+1)}{6}$.
(2)①S3=$\frac{1}{3}$•($\frac{1}{3}$)2+$\frac{1}{3}$•($\frac{2}{3}$)2+$\frac{1}{3}$($\frac{3}{3}$)2=$\frac{1}{27}$(12+22+32)=$\frac{14}{27}$.
②由①可知Sn=$\frac{1}{{n}^{3}}$(12+22+32+…+n2)=$\frac{n(n+1)(2n+1)}{6{n}^{3}}$.
③∵Sn=$\frac{1}{{n}^{3}}$(12+22+32+…+n2)=$\frac{n(n+1)(2n+1)}{6{n}^{3}}$=$\frac{2{n}^{3}+{3n}^{2}+n}{6{n}^{3}}$=$\frac{1}{3}$+$\frac{1}{2n}$+$\frac{1}{6{n}^{2}}$,
∵n充分大时,$\frac{1}{2n}$、$\frac{1}{6{n}^{2}}$接近于0,
∴Sn的值逼近于$\frac{1}{3}$,
∴S=$\frac{1}{3}$.
(3)如图4中,设抛物线y=2x2与直线y=2x+4的交点为A、B,作AE⊥x轴于E,BF⊥x轴于F.记曲边三角形AEO的面积为S1,曲边三角形OBF的面积为S2.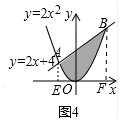
由$\left\{\begin{array}{l}{y=2{x}^{2}}\\{y=2x+4}\end{array}\right.$交点$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=8}\end{array}\right.$,
∴A(-1,2),B(2,8),E(-1,0),F(2,0),
将底边EO分成n等分,构建n个矩形
S1=$\frac{1}{n}$•2•($\frac{1}{n}$)2+$\frac{1}{n}$•2•($\frac{2}{n}$)2+…+$\frac{1}{n}$•2•($\frac{n}{n}$)2=$\frac{2}{{n}^{3}}$(1+22+32+…+n2),
由(2)
可知S1逼近于$\frac{2}{3}$,同理可得S2逼近于$\frac{16}{3}$,
∴S阴=S梯形AEFB-S1-S2=$\frac{2+8}{2}$•3-$\frac{2}{3}$-$\frac{16}{3}$=9.
点评 本题考查二次函数综合题,矩形的性质、逼近法求面积等知识,解题的关键是理解题意,学会模仿例题解决问题,属于创新题目,中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
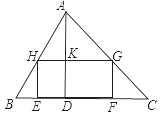 有一块三角形的余料ABC,要把它加工成矩形的零件,已知,BC=12cm,高AD=8cm,矩形EFGH的边EF在BC边上,G、H分别在AC、AB上.
有一块三角形的余料ABC,要把它加工成矩形的零件,已知,BC=12cm,高AD=8cm,矩形EFGH的边EF在BC边上,G、H分别在AC、AB上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
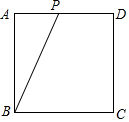 正方形ABCD的边长为2,点P是边AD上一动点(不与点A、D重合),设AP=x.
正方形ABCD的边长为2,点P是边AD上一动点(不与点A、D重合),设AP=x.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com