
【题目】中国古代有二十四节气歌,“春雨惊春清谷天,夏满芒夏暑相连.秋处露秋寒霜降,冬雪雪冬小大寒.”它是为便于记忆我国古时历法中二十四节气而编成的小诗歌,流传至今.节气指二十四时节和气候,是中国古代订立的一种用来指导农事的补充历法,是中国古代劳动人民长期经验的积累和智慧的结晶.其中第一个字“春”是指立春,为春季的开始,但在气象学上的入春日是有严格定义的,即连续5天的日平均气温稳定超过10℃又低于22℃,才算是进入春天,其中,5天中的第一天即为入春日.例如:2014年3月13日至18日,北京的日平均气温分别为9.3℃,11.7℃,12.7℃,11.7℃,12.7℃和12.3℃,即从3月14日开始,北京日平均气温已连续5天稳定超过10℃,达到了气象学意义上的入春标准.因此可以说2014年3月14日为北京的入春日. 日平均温度是指一天24小时的平均温度.气象学上通常用一天中的2时、8时、14时、20时4个时刻的气温的平均值作为这一天的日平均气温(即4个气温相加除以4),结果保留一位小数.
如表是北京顺义2017年3月28日至4月3日的气温记录及日平均气温(单位:℃)
时间 | 2时 | 8时 | 14时 | 20时 | 平均气温 |
3月28日 | 6 | 8 | 13 | 11 | 9.5 |
3月29日 | 7 | 6 | 17 | 14 | a |
3月30日 | 7 | 9 | 15 | 12 | 10.8 |
3月31日 | 8 | 10 | 19 | 13 | 12.5 |
4月1日 | 8 | 7 | 18 | 15 | 12 |
4月2日 | 11 | 7 | 22 | 16 | 14 |
4月3日 | 13 | 11 | 21 | 17 | 15.5 |
根据以上材料解答下列问题:
(1)求出3月29日的日平均气温a;
(2)采用适当的统计图将这7天的日平均气温的变化情况表示出来;
(3)请指出2017年的哪一天是北京顺义在气象学意义上的入春日.
【答案】
(1)解:a= ![]() =11(℃)
=11(℃)
(2)解:如图所示,

(3)解:2017年的3月29日是北京顺义在气象学意义上的入春日
【解析】(1)根据算术平均数的求法即可得到结论;(2)根据题意绘制统计图;(3)根据题意即可得到结论.
【考点精析】本题主要考查了统计图的选择和算术平均数的相关知识点,需要掌握条形统计图便于直观了解数据的大小及不同数据的差异;折线统计图便于直观了解数据的变化趋势,同时也便于了解数据的多少;扇形统计图便于直观了解各部分数量与总数的百分比,以及部分与部分之间的大小关系;总数量÷总份数=平均数.解题关键是根据已知条件确定总数量以及与它相对应的总份数才能正确解答此题.


科目:初中数学 来源: 题型:
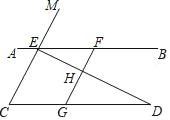
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正五边形广场 ![]() 的边长为
的边长为 ![]() 米,甲、乙两个同学做游戏,分别从
米,甲、乙两个同学做游戏,分别从 ![]() 、
、 ![]() 两点处同时出发,沿
两点处同时出发,沿 ![]() 的方向绕广场行走,甲的速度为
的方向绕广场行走,甲的速度为 ![]() ,乙的速度为
,乙的速度为 ![]() ,则两人第一次刚走到同一条边上时( )
,则两人第一次刚走到同一条边上时( )
A. 甲在顶点 ![]() 处 B. 甲在顶点
处 B. 甲在顶点 ![]() 处 C. 甲在顶点
处 C. 甲在顶点![]() 处 D. 甲在顶点
处 D. 甲在顶点![]() 处
处
查看答案和解析>>
科目:初中数学 来源: 题型:
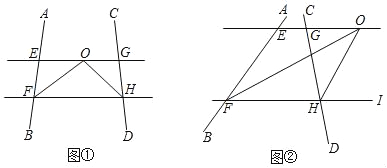
【题目】(探究)如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF=_____度,∠FOH=_____度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
(拓展)如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为: ;
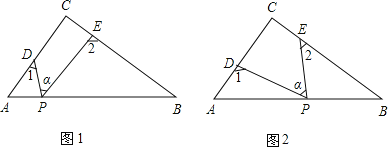
(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.

(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间的关系为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,对角线AC,BD相交于点O,AB=AC=AD,∠DAC=∠ABC. 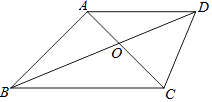
(1)求证:BD平分∠ABC;
(2)若∠DAC=45°,OA=1,求OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
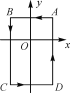
【题目】如图,在平面直角坐标系中:A(1,1),B(-1,1),C(-1,-2),D(1,-2),现把一条长为2 018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
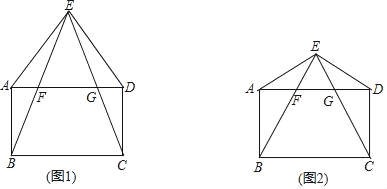
【题目】已知:点E为矩形ABCD外一点,连接AE,DE,且AE=DE,连接EB,EC分别与AD相交于点F,G.
(1)如图1,求证:∠ABE=∠DCE;
(2)如图2,若△BCE是等边三角形,且AE=AB,在不添加任何辅助线的情况下,请直接写出图2中四对全等的钝角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com