
【题目】如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F.

(1)求证:△APD≌△CPD;
(2)求证:△APE∽△FPA;
(3)若PE=2,EF=6,求PC的长.
【答案】(1)见解析;(2)见解析;(3)PC=4
【解析】
(1)利用菱形的性质结合条件可证明△APD≌△CPD;
(2)根据全等三角形的性质得到∠DAP=∠DCP,根据平行线的性质得到∠DCP=∠F,等量代换得到∠DAP=∠F,可得△APE∽△FPA;
(3)根据相似三角形的性质得到![]() ,于是得到PA2=PEPF,等量代换即可得到PC2=PEPF,求得PC=4.
,于是得到PA2=PEPF,等量代换即可得到PC2=PEPF,求得PC=4.
(1)证明:∵四边形ABCD菱形,
∴AD=CD,∠ADP=∠CDP,
在△APD和△CPD中,
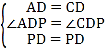 ,
,
∴△APD≌△CPD(SAS);
(2)∵△APD≌△CPD,
∴∠DAP=∠DCP,
∵CD∥BF,
∴∠DCP=∠F,
∴∠DAP=∠F,
又∵∠APE=∠FPA,
∴△APE∽△FPA,
(3)∵△APE∽△FPA
∴![]() ,
,
∴PA2=PEPF,
∵△APD≌△CPD,
∴PA=PC,
∴PC2=PEPF,
∵PE=2,EF=6,
∴PF=PE+EF=2+6=8,
∴PC=4.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
【题目】为建设天府新区“公园城市”,实现城市生活垃圾减量化、资源化、无害化的目标.近日,成都市天府新区计划在各社区试点实施生活垃圾分类处理活动,取得市民积极响应.某创业公司发现这一商机,研发生产了一种新型家庭垃圾分类桶,并投入市场试营销售.已知该新型垃圾桶成本为每个40元,市场调查发现,该垃圾桶每件售价y(元)与每天的销售量为x(个)的关系如图.为推广新产品及考虑每件利润因素,公司计划每天的销售量不低于1000件且不高于2000件.
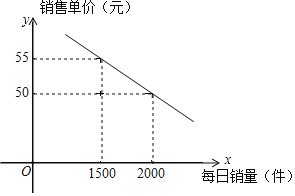
(1)求每件销售单价y(元)与每天的销售量为x(个)的函数关系式;
(2)设该公司日销售利润为W(元),求每天的最大销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,一元二次方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2×i=(﹣1)×i=﹣i,i4=(i2)2=(﹣1)2=1,从而对任意正整数n,我们可以得到i4n+1=i4n×i=(i4)n×i=i,i4n+2=﹣1,i4n+3=﹣i,i4n=1.那么i+i2+i3+i4+…+i2012+i2013+…+i2019的值为( )
A.0B.1C.﹣1D.i
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象上有一动点
的图象上有一动点![]() ,连接
,连接![]() 并延长交图象的另一支于点
并延长交图象的另一支于点![]() ,在第二象限内有一点
,在第二象限内有一点![]() ,满足
,满足![]() ,当点
,当点![]() 运动时,点
运动时,点![]() 始终在函数
始终在函数![]() 的图象上运动,
的图象上运动,![]() ,则
,则![]() ______.
______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,BE=FC,CF=2FD,AE、BF交于点G,连接AF,给出下列结论:①AE⊥BF; ②AE=BF; ③BG=![]() GE; ④S四边形CEGF=S△ABG,其中正确的个数为( )
GE; ④S四边形CEGF=S△ABG,其中正确的个数为( )
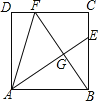
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的大小是( )
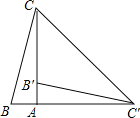
A.32°B.64°C.77°D.87°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣2ax+m的图象经过点P(4,5),与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,且S△PAB=10.
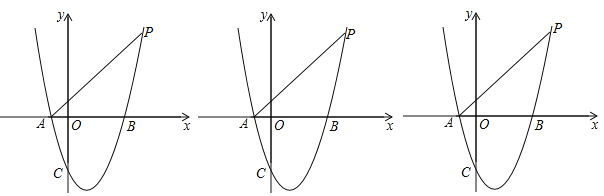
(1)求抛物线的解析式;
(2)在抛物线上是否存在点Q使得△PAQ和△PBQ的面积相等?若存在,求出Q点的坐标,若不存在,请说明理由;
(3)过A、P、C三点的圆与抛物线交于另一点D,求出D点坐标及四边形PACD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差.如图1,在△ABC中,AO是BC边上的中线,AB与AC的“极化值”就等于AO2﹣BO2的值,可记为AB△AC=AO2﹣BO2.
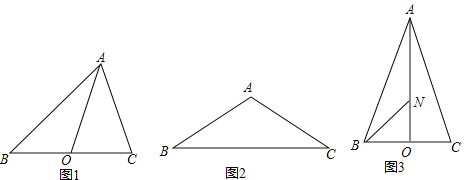
(1)在图1中,若∠BAC=90°,AB=8,AC=6,AO是BC边上的中线,则AB△AC= ,OC△OA= ;
(2)如图2,在△ABC中,AB=AC=4,∠BAC=120°,求AB△AC、BA△BC的值;
(3)如图3,在△ABC中,AB=AC,AO是BC边上的中线,点N在AO上,且ON=![]() AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
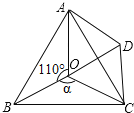
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当△AOD是直角三角形且∠ADO=90°时,求α的度数;
(3)当α=110°或125°或140°时,判断△AOD的形状,请选择其中一种情况说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com