Question

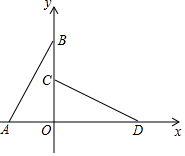
13．将Rt△AOB 如图放置在直角坐标系中，并绕O点顺时针旋转90°至△COD的位置，已知A（-2，0），∠ABO=30°．则△AOB旋转过程中所扫过的图形的面积为（　　）

• A． $\frac{11π}{3}+2\sqrt{3}$
• B． $3π+2\sqrt{3}$
• C． $3π+\sqrt{3}$
• D． $\frac{11π}{3}+\sqrt{3}$

Answer 1

分析 由A（-2，0），得到OA=2，求得OB=2$\sqrt{3}$，∠BAO=60°根据三角形和扇形的面积公式即可得到结论；

解答 解：∵A（-2，0），
∴OA=2，
∵∠ABO=30°，
∴OB=2$\sqrt{3}$，∠BAO=60°，
∴△AOB旋转过程中所扫过的图形的面积=S_△BC′M+S_扇形AOC′+S_扇形BOD=$\frac{1}{2}×$1×2$\sqrt{3}$+$\frac{60•π×{2}^{2}}{360}$+$\frac{90•π×（2\sqrt{3}）^{2}}{360}$=$\frac{11}{3}$π+$\sqrt{3}$，
故选D．

点评 此题考查了作图-旋转变换及扇形面积的计算，熟记扇形的面积公式是解题的关键．