
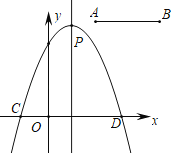
����Ŀ����ͼ���߶�AB��A��2��3����B��5��3����������y������x��1��2��m2+2m+1��x�����������ֱ�ΪC��D����C�ڵ�D����ࣩ
��1����mΪ��ֵʱ�����߹�ԭ�㣬�������ʱ�����ߵĽ���ʽ���Գ����������꣮
��2���������ߵĶ���ΪP��mΪ��ֵʱ��PCD���������������Ƕ��٣�
��3�����߶�AB��y������ƽ��n����λ����m��n�������Ĺ�ϵʱ���������ܰ��߶�AB�ֳ�1��2�����֣�
���𰸡���1����m��0��m��2ʱ�������߹�ԭ�㣬��ʱ�����ߵĽ���ʽ��y������x��1��2+1���Գ���Ϊֱ��x��1������Ϊ��1��1������2��mΪ1ʱ��PCD����������������2![]() ����3��n��m2��2m+6��n��m2��2m+11��
����3��n��m2��2m+6��n��m2��2m+11��
��������
��1�����������߹�ԭ�����Ŀ�еĺ�������ʽ�������m��ֵ���������ʱ�����ߵĽ���ʽ���Գ����������ꣻ
��2��������Ŀ�еĺ�������ʽ�Ͷ��κ��������ʣ��������mΪ��ֵʱ��PCD����������õ�C��D�����꣬�ɴ������PCD��������ֵ��
��3�����������������ܰ��߶�AB�ֳ�1��2����������������������������߶�AB�������ߵĽ��㣬���ɵõ���m��n�������Ĺ�ϵʱ���������ܰ��߶�AB�ֳ�1��2�����֣�
��1����y������x��1��2��m2+2m+1��ԭ�㣨0��0��ʱ��0����1��m2+2m+1����m1��0��m2��2��
��m1��0ʱ��y������x��1��2+1��
��m2��2ʱ��y������x��1��2+1��
���Ͽɵã���m��0��m��2ʱ�������߹�ԭ�㣬��ʱ�����ߵĽ���ʽ��y������x��1��2+1���Գ���Ϊֱ��x��1������Ϊ��1��1����
��2����������y������x��1��2��m2+2m+1��
��������ߵĶ���PΪ��1����m2+2m+1����
����m2+2m+1���ʱ����PCD��������
�ߩ�m2+2m+1������m��1��2+2��
�൱m��1ʱ����m2+2m+1���Ϊ2��
��y������x��1��2+2��
��y��0ʱ��0������x��1��2+2����x1��1+![]() ��x2��1��
��x2��1��![]() ��
��
���C��������1��![]() ��0������D��������1+
��0������D��������1+![]() ��0��
��0��
��CD����1+![]() ������1��
������1��![]() ����2
����2![]() ��
��
��S��PCD��![]() ��2
��2![]() ��
��
��mΪ1ʱ��PCD����������������2![]() ��
��
��3�����߶�AB��y������ƽ��n����λA��2��3��n����B��5��3��n��
���߶�AB�ֳ�1��2�����֣���㣨3��3��n����4��3��n���ڸ������߽���ʽ�ϣ�
�ѣ�3��3��n�����������߽���ʽ�ã�
3��n������3��1��2��m2+3m+1��
��n��m2��2m+6��
�ѣ�4��3��n�����������߽���ʽ����
3��n������3��1��2��m2+3m+1��
��n��m2��2m+11��
��n��m2��2m+6��n��m2��2m+11��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����C�ǡ�O��һ�㣬D��![]() ���е㣬EΪOD�ӳ�����һ�㣬�ҡ�CAE��2��C��AC��BD���ڵ�H����OE���ڵ�F��
���е㣬EΪOD�ӳ�����һ�㣬�ҡ�CAE��2��C��AC��BD���ڵ�H����OE���ڵ�F��
��1����֤��AE�ǡ�O�����ߣ�
��2����DH��9��tanC��![]() ����ֱ��AB�ij���
����ֱ��AB�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊ��Ӫ����Ƿ��68400Ԫ����Ϣ�����ծ����ת�о�Ӫ��װר������ȱ���ʽ𣮡��й������㡱��Ŀ���������õ�30000Ԫ�ʽ𣬲�Լ�����þ�Ӫ������ծ������ծ���������Ϣ������֪�õ������Ʒ�Ʒ�װ�Ľ���Ϊÿ��40Ԫ����Ʒ�Ʒ�װ��������![]() �����������ۼ�
�����������ۼ�![]() ��Ԫ����֮��Ĺ�ϵ����ͼ�е�һ�����ߣ�ʵ�ߣ�����ʾ���õ�Ӧ֧��Ա���Ĺ���Ϊÿ��ÿ��82Ԫ��ÿ�컹Ӧ֧����������Ϊ106Ԫ��������ծ��
��Ԫ����֮��Ĺ�ϵ����ͼ�е�һ�����ߣ�ʵ�ߣ�����ʾ���õ�Ӧ֧��Ա���Ĺ���Ϊÿ��ÿ��82Ԫ��ÿ�컹Ӧ֧����������Ϊ106Ԫ��������ծ��
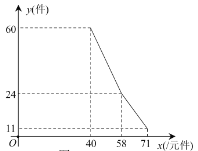
��1������������![]() �����������ۼ�
�����������ۼ�![]() ��Ԫ/����֮��ĺ�����ϵʽ��
��Ԫ/����֮��ĺ�����ϵʽ��
��2�����õ��ݲ����dz���ծ��ij������ۼ�Ϊ48Ԫ/��ʱ������������֧ƽ�⣨����=֧��������õ�Ա����������
��3�����õ�ֻ��2��Ա������õ�������Ҫ�������ܻ�������ծ��ʱÿ����װ�ļ۸�Ӧ��Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
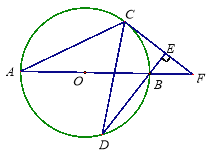
����Ŀ����ͼ��ABΪ��Oֱ����C��DΪ��O����ͬ��A��B����������ABD=2��BAC������CD.����C��CE��DB������ΪE��ֱ��AB��CE�ཻ��F��.
��1����֤��CFΪ��O��������
��2����BF=5,![]() ʱ����BD�ij�.
ʱ����BD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������OABC�ı߳�Ϊ4�������ڲ������ϵĺᡢ�������Ϊ�����ĵ��Ϊ���㣬��PΪ������![]() �Ķ��㣨mΪ������������P��������OABC�ڲ������ʱ���������·��������߽磩�����������У�������
�Ķ��㣨mΪ������������P��������OABC�ڲ������ʱ���������·��������߽磩�����������У�������
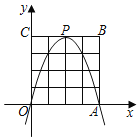
A.3��B.5��C.10��D.15��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������ֱ��A��B����ͬʱ�������׳�����ǰ��B�أ�����B����������һ�ٶȰ�ԭ·���ٷ��ص�A�أ��ҳ�����ǰ��A�أ���ס�����������A�صľ���Ϊy(km)���׳���ʻ��ʱ��Ϊx(h)��y��x֮��ĺ���ͼ����ͼ��ʾ��

��1���׳���A��ǰ��B�ص��ٶ�Ϊ______km/h��
��2����׳�����ʱy��x֮��ĺ�����ϵʽ��
��3�����ס����������50kmʱ��ֱ��д���׳���ʻ��ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �Ƿ���ʵ����
�Ƿ���ʵ����![]() ����ͬһƽ��ֱ������ϵ�У����κ���
����ͬһƽ��ֱ������ϵ�У����κ���![]() ��һ�κ���
��һ�κ���![]() �Ĵ���ͼ�����ǣ� ��
�Ĵ���ͼ�����ǣ� ��
A.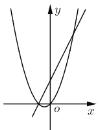 B.
B.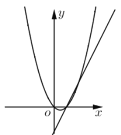 C.
C.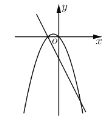 D.
D.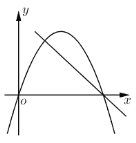
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
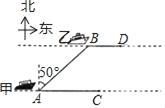
����Ŀ����ͼ�������ϼס��������ֱ��A��B����ͬʱ��������������ʻ���״����ٶ�Ϊ24n mile/h���Ҵ����ٶ�Ϊ15n mile/h������ʱ������Ҵ��ڼ״���ƫ��50�㷽����AB=10nmile������20���Ӻס��������ֱ�C��D������
���ο�ֵ��sin50����0.766��cos50���0.643��tan50���1.192��
��1������������ľ��룻
��2������������ԭ�����ٶȺͺ�����Ҫ����ʱ�����ʹ�����ľ�����̣�����ȷ��0.01��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ҹ��Ĵ�ͳ���գ��������г����ӵ�ϰ�ף�ij�̳��ڶ��������֮����3000Ԫ����![]() ��
��![]() ��������1100��������
��������1100��������![]() �������빺��
�������빺��![]() �����ӵķ�����ͬ����֪
�����ӵķ�����ͬ����֪![]() ���ӵĵ�����
���ӵĵ�����![]() �����ӵ��۵�1.2��.
�����ӵ��۵�1.2��.
��1����![]() ��
��![]() �������ӵĵ��۸��Ƕ��٣�
�������ӵĵ��۸��Ƕ��٣�
��2�����ƻ��ò�����7000Ԫ���ʽ��ٴι���![]() ��
��![]() �������ӹ�2600������֪
�������ӹ�2600������֪![]() ��
��![]() �������ӵĽ��۲��䣬��
�������ӵĽ��۲��䣬��![]() ����������ܹ������ٸ���
����������ܹ������ٸ���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com