
【题目】如图,在线段![]() 上任取一点
上任取一点![]() ,将线段
,将线段![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,将线段
,将线段![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .直线
.直线![]() 分别交
分别交![]() ,
,![]() 于
于![]() ,
,![]() 两点,有下列结论:①
两点,有下列结论:①![]() ;②四边形
;②四边形![]() 为平行四边形;③
为平行四边形;③![]() ;④
;④![]() .其中正确的结论是( )
.其中正确的结论是( )
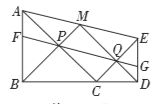
A.①③④B.①②③C.②③④D.①②③④
【答案】D
【解析】
①过点M作MN⊥BD,垂足为N,则MN∥DE∥AB,根据平行线分线段成比例定理得出N为BD中点,由线段垂直平分线的性质得到BM=DM,再根据梯形中位线、等腰直角三角形的性质得出MN=![]() BD,则∠BMD=90°,判断①正确;
BD,则∠BMD=90°,判断①正确;
②先由等腰直角三角形的性质及三角形内角和定理得出∠BPC=90°,再根据等腰三角形三线合一的性质得出AP=PC,同理得出EQ=QC,则PQ是△CAE的中位线,由三角形中位线定理得到PQ∥AE,PQ=![]() AE,又AF∥EG,根据两组对边分别平行的四边形是平行四边形可判断②正确;
AE,又AF∥EG,根据两组对边分别平行的四边形是平行四边形可判断②正确;
③先由平行四边形的性质得出FG=AE,又由②知PQ=![]() AE,则FP+GQ=
AE,则FP+GQ=![]() AE=PQ,判断③正确;
AE=PQ,判断③正确;
④先证明∠APF=∠DQG,又∠FAP=∠GDQ=45°,根据两角对应相等的两三角形相似得出△APF∽△DQG,由相似三角形对应边成比例得出![]() ,同理△BPF∽△EQG,
,同理△BPF∽△EQG,![]() ,则
,则![]() ,AFEG=BFDG,又AF=EG,判断④正确.
,AFEG=BFDG,又AF=EG,判断④正确.
解:①过点M作MN⊥BD,垂足为N,则MN∥DE∥AB,
∵点M是AE的中点,
∴N为BD中点,即MN垂直平分BD,
∴BM=DM.
∵MN是梯形ABDE的中位线,
∴MN=![]() (AB+ED)=
(AB+ED)=![]() (BC+CD)=
(BC+CD)=![]() BD=BN=ND,
BD=BN=ND,
∴∠BMD=90°,
即BM⊥DM,故①正确;
②∵△BMD、△ABC均是等腰直角三角形,
∴∠MBD=∠ACB=45°,
∴∠BPC=90°,即BP⊥AC,
∴AP=PC,
同理EQ=QC,
∴PQ是△CAE的中位线,
∴PQ∥AE,PQ=![]() AE,
AE,
又∵AF∥EG,
∴四边形AFGE为平行四边形,故②正确;
③∵四边形AFGE为平行四边形,
∴FG=AE,
∵PQ=![]() AE,
AE,
∴FP+GQ=FG-PQ=AE-![]() AE=
AE=![]() AE=PQ,
AE=PQ,
即FP+GQ=PQ,故③正确;
④∵∠ACB=∠MDB=45°,
∴AC∥DM,
∴∠CPQ=∠MQP,
∵∠APF=∠CPQ,∠MQP=∠DQG,
∴∠APF=∠DQG,
∵∠FAP=∠GDQ=45°,
∴△APF∽△DQG,
∴![]() ,
,
同理△BPF∽△EQG,
∴![]() ,
,
∴![]() ,
,
∴AFEG=BFDG,
∵四边形AFEG是平行四边形,
∴AF=EG,
∴AF2=BFDG,故④正确.
故选:D.


科目:初中数学 来源: 题型:
【题目】如图某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
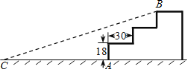
A.270cmB.210cmC.180cmD.96cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有高度相同的一段方木和一段圆木,体积之比是1:1.在高度不变的情况下,如果将方木加工成尽可能大的圆柱,将圆木加工成尽可能大的长方体,则得到的圆柱和长方体的体积之比为____.
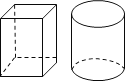
查看答案和解析>>
科目:初中数学 来源: 题型:
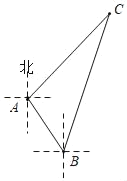
【题目】如图,某考察船在某海域进行科考活动,在点A测得小岛C在它的东北方向上,它沿南偏东37°方向航行了2海里到达点B处,又测得小岛C在它的北偏东23°方向上.
(1)求∠C的度数;
(2)求该考察船在点B处与小岛C之间的距离.(精确到0.1海里)
(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() =1.41,
=1.41,![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在信息快速发展的新时代,“信息消费”已成为人们生活的重要部分.为了解某社区居民每月信息消费的情况,学校社会实践小组到该社区随机调查了部分住户2019年7月的信息消费金额,并将手机到的数据整理成不完整统计图(图9.1、图9.2).
请结合图中相关数据回答下列问题.

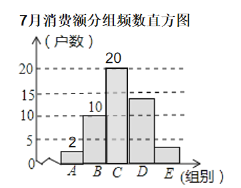

(1)本次调查样本的容量是______;
(2)D组的频数是______,E组的频率是______,B组所对应扇形的圆心角为______度;
(3)在调查的住户中,当月信息消费金额的中位数出现在______组;
(4)若该社区有1500户住户,估计当月信息消费额不少于300元的约有______户.
查看答案和解析>>
科目:初中数学 来源: 题型:
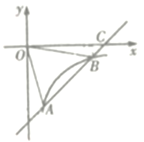
【题目】如图,已知一次函数y= kx +b的图象交反比例函数![]() 的图象于点A(2,-4)和点B(h,-2),交x轴于点C.
的图象于点A(2,-4)和点B(h,-2),交x轴于点C.
(1)求这两个函数的解析式;
(2)连接QA、OB.求△AOB的面积;
(3)请直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
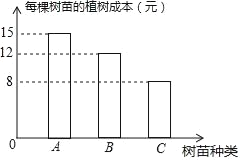
【题目】现种植A、B、C三种树苗一共480棵,安排80名工人一天正好完成,已知每名工人只植一种树苗,且每名工人每天可植A种树苗8棵;或植B种树苗6棵,或植C种树苗5棵.经过统计,在整个过程中,每棵树苗的种植成本如图所示.设种植A种树苗的工人为x名,种植B种树苗的工人为y名.
(1)求y与x之间的函数关系式;
(2)设种植的总成本为w元,
①求w与x之间的函数关系式;
②若种植的总成本为5600元,从植树工人中随机采访一名工人,求采访到种植C种树苗工人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的对角线
的对角线![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() 轴于点
轴于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
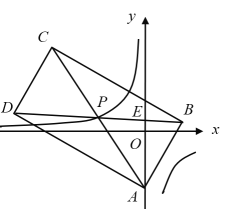
(1)求![]() 的值;
的值;
(2)若将矩形![]() 向下平移
向下平移![]() 个单位,使点
个单位,使点![]() 落在反比例函数
落在反比例函数![]() 的图象上,求
的图象上,求![]() 的值;
的值;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:若抛物线的顶点在坐标轴上,则称该抛物线为“数轴函数”例如抛物线y=x2和y=(x-1)2都是“数轴函数”.
(1)抛物线y=x2-4x+4和抛物线y=x2-6x是“数轴函数“吗?请说明理由;
(2)若抛物线y=2x2+4mx+m2+16是“数轴函数”,求该抛物线的表达式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com