
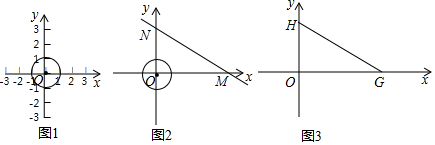
分析 (1)①利用图象法即可得出结论.②取特殊点P(3,0)即可解决问题;
(2)当点A在⊙O内部时,点A必为价值点,当点A在⊙O外部时,由⊙O的半径为1,推出BC的最大值为2,人2点A为价值点,则AB=CB=2,可知OA=3,故以O为圆心,半径为3的圆内的点(不包括⊙O上的点)均为价值点,由此即可解决问题;
(3)当⊙C的圆心在点O时,HG上恰好存在⊙C的价值点K,因为⊙C的价值点是在以点C为圆心,半径为3的圆内(不包括⊙C上的点),易知当点C的坐标为(9,0)时,⊙C的价值点为点C;
解答 解:(1)①如图1中,观察图象可知,D、E是⊙O的价值点.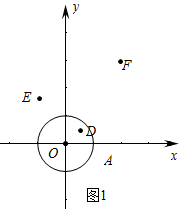
②如图2中,当P点坐标为(3,0)时,x的值最大.x的最大值为3.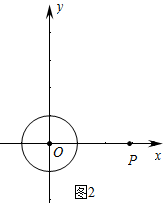
故答案为D,E;3.
(2)当点A在⊙O内部时,点A必为价值点,
当点A在⊙O外部时,∵⊙O的半径为1,
∴BC的最大值为2,人2点A为价值点,则AB=CB=2,
∴OA=3,
故以O为圆心,半径为3的圆内的点(不包括⊙O上的点)均为价值点,
对于函数y=-$\frac{\sqrt{3}}{3}$x+3,令y=0,则x=3$\sqrt{3}$,
∴M(3$\sqrt{3}$,0),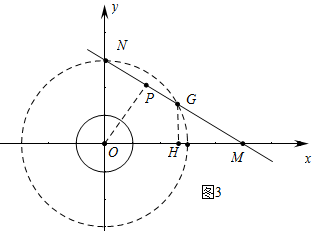
令x=0,则y=3,∴N(0,3),
∴tan∠ONM=$\frac{OM}{ON}$=$\frac{3\sqrt{3}}{3}$=$\sqrt{3}$,
∴∠ONM=60°,
∴OP=ON•sin∠ONM=3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$>1,
∴直线MN上的点均在圆外,
如图3中,以O为圆心,ON为半径画圆,交直线MN于点G,则OG=ON=3,
∴⊙O的价值点必在线段NG上,
∵∠ONM=60°,OG=ON=3,
∴△ONG是等边三角形,
∴∠NOG=60°,∴∠MOG=30°,
过点G作GH⊥OM于点H
∵OG=3,
∴OH=OG•cos30°=$\frac{3\sqrt{3}}{2}$,
∴价值点横坐标的取值范围为0≤x≤$\frac{3\sqrt{3}}{2}$.
(3)对于函数y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$,
令y=0,则x=6,
∴G(6,0),
令x=0,则y=2$\sqrt{3}$,
∴H(0,2$\sqrt{3}$),
∴tan∠HGO=$\frac{OH}{OG}$=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$,
∴∠HGO=30°,
过点O作OK⊥HG于K,则OK=$\frac{1}{2}$OG=3,
∴当⊙C的圆心在点O时,HG上恰好存在⊙C的价值点K,
∵⊙C的价值点是在以点C为圆心,半径为3的圆内(不包括⊙C上的点),
∴当点C的坐标为(9,0)时,⊙C的价值点为点C,
∴圆心C的横坐标的取值范围为0≤x≤9.
点评 本题考查圆的综合问题,解题关键是根据相邻点的定义,得出点P与圆心C的距离范围,本题涉及相似三角形的性质与判定,圆的性质等知识,综合程度较高,需要学生认真理解题意.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
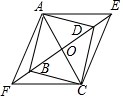 如图,在?ABCD中,对角线AC、BD相交于点O,OA=5cm,E、F为直线BD上的两个动点(点E、F始终在?ABCD的外面),且DE=$\frac{1}{2}$OD,BF=$\frac{1}{2}$OB,连接AE、CE、CF、AF.
如图,在?ABCD中,对角线AC、BD相交于点O,OA=5cm,E、F为直线BD上的两个动点(点E、F始终在?ABCD的外面),且DE=$\frac{1}{2}$OD,BF=$\frac{1}{2}$OB,连接AE、CE、CF、AF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com