
【题目】如图,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,C是AB的中点,且a、b满足|a+3|+(b+3a)2=0.
(1)求点C表示的数;
(2)点P从A点以3个单位每秒向右运动,点Q同时从B点以2个单位每秒向左运动,若AP+BQ=2PQ,求时间t;
(3)若点P从A向右运动,点M为AP中点,在P点到达点B之前:①![]() 的值不变;②2BM﹣BP的值不变,其中只有一个正确,请你找出正确的结论并求出其值.
的值不变;②2BM﹣BP的值不变,其中只有一个正确,请你找出正确的结论并求出其值.
![]()
【答案】(1)3;(2)![]()
![]() (3)12.
(3)12.
【解析】试题分析:(1)先根据非负数的性质求出a,b的值,再根据中点的定义得出点C表示的数即可;
(2)先用t表示出AP,BQ及PQ的值,再根据AP+BQ=2PQ列出关于t的方程,求出t的值即可;
(3)先根据PA+PB=AB,BM=PB+![]() 即可得出结论.
即可得出结论.
试题解析:
解:(1)∵|a+3|+(b+3a)2=0,
∴a+3=0,b+3a=0,解得a=﹣3,b=9,
∴![]() =3,
=3,
∴点C表示的数是3;
(2)∵AB=9-(-3)=12,点P从A点以3个单位每秒向右运动,点Q同时从B点以2个单位每秒向左运动,
∴AP=3t,BQ=2t,PQ=12﹣5t.
∵AP+BQ=2PQ,
∴3t+2t=24﹣10t,解得t=![]() ;
;
还有一种情况,当P运动到Q的左边时,PQ=5t﹣12,方程变为2t+3t=2(5t﹣12),求得t=![]() .
.
(3)∵PA+PB=AB为定值,PC先变小后变大,
∴![]() 的值是变化的,
的值是变化的,
∴①错误,②正确;
∵BM=PB+![]() ,
,
∴2BM=2PB+AP,
∴2BM﹣BP=PB+AP=AB=12.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:初中数学 来源: 题型:
【题目】把多项式x2+ax+b分解因式,得(x+1)(x-3)则a , b的值分别是( )
A.a=2,b=3
B.a=-2,b=-3
C.a=-2,b=3
D.a=2,b=-3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2mx以下各点不可能成为二次函数顶点的是( )
A. (﹣2,4) B. (﹣2,﹣4) C. (﹣1,﹣1) D. (1,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖北襄阳第8题)如图,I是ABC的内心,AI向延长线和△ABC的外接圆相交于点D,连接BI,BD,DC下列说法中错误的一项是( )[
A.线段DB绕点D顺时针旋转一定能与线段DC重合
B.线段DB绕点D顺时针旋转一定能与线段DI熏合
C.∠CAD绕点A顺时针旋转一定能与∠DAB重合
D.线段ID绕点I顺时针旋转一定能与线段IB重合
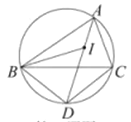
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )
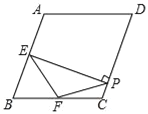
A. 50° B. 55° C. 60° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山东省聊城市第19题)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A1B2C2关于原点O成中心对称图形,写出△A1B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A2B3C3,写出△A2B3C3的各顶点的坐标.
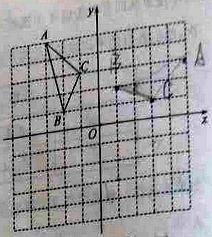
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下面给出的数轴,解答下面的问题:

(1)请你根据图中A、B两点的位置,分别写出它们所表示的有理数
A: ___________ B: _____________ ;
(2)观察数轴,与点A的距离为3的点表示的数是:_____________ ;
(3)若将数轴折叠,使得A点与-3表示的点重合,则B点与数_ _表示的点重合;
(4)若数轴上M、N两点之间的距离为1004(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是: M: _______ N: _______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(1)第1个等式:a1=![]() ; 第2个等式:a2=
; 第2个等式:a2=![]() ;
;
第3个等式:a3=![]() ; 第4个等式:a4=
; 第4个等式:a4=![]() ;
;
…
用含有n的代数式表示第n个等式:an=___________=___________(n为正整数);
(2)按一定规律排列的一列数依次为![]() ,1,
,1, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,…,按此规律,这列数中的第100个数是_______________.
,…,按此规律,这列数中的第100个数是_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com