
【题目】在一个蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)的关系如图所示,请根据图像提供的信息解答下列问题.
(1)甲、乙两根蜡烛燃烧前的高度分别是____________,从点燃到燃尽所用的时间分别是__________;
(2)分别求甲、乙两根蜡烛燃烧时,y与x之间的函数表达式;
(3)当x为何值时,甲、乙两根蜡烛在燃烧过程中的高度相等?

【答案】(1)30cm,25cm;2h,2.5h;(2)y甲=30-15x(0≤x≤2),y乙=25-10x(0≤x≤2.5);(3) 1
【解析】【试题分析】(1)由图像可知,甲根蜡烛燃烧前的高度分别是30cm,从点燃到燃尽所用的时间分别是2h;乙根蜡烛燃烧前的高度分别是25cm,从点燃到燃尽所用的时间分别是2.5h;(2)甲燃烧的速度为15cm/h,乙燃烧的速度为10cm/h,易得答案;(3)由(2)得出方程求解即可.
【试题解析】
(1))由图像可知,甲根蜡烛燃烧前的高度分别是30cm,从点燃到燃尽所用的时间分别是2h;乙根蜡烛燃烧前的高度分别是25cm,从点燃到燃尽所用的时间分别是2.5h;
(2)甲燃烧的速度为15cm/h,乙燃烧的速度为10cm/h,易得y甲=30-15x(0≤x≤2),y乙=25-10x(0≤x≤2.5);
(3)由题意得:30-15x=25-10x,解得: ![]() .
.
故答案:(1)30cm,25cm;2h,2.5h;(2)y甲=30-15x(0≤x≤2),y乙=25-10x(0≤x≤2.5);(3) 1.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】(本题满分7分)在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A处。另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,求这棵树高。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣3x+ ![]() 与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E 
(1)求A、B的坐标;
(2)求直线BC的解析式;
(3)当线段DE的长度最大时,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.
(1)如图1,若P为AB边上一点以PD,PC为边作平行四边形PCQD,请问对角线PQ的长是否存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
(2)若P为AB边上任意一点,延长PD到E,使DE=PD,再以PE,PC为边作平行四边形PCQE,请问对角线PQ的长是否也存在最小值?如果存在,请直接写出最小值,如果不存在,请说明理由.
(3)如图2,若P为直线DC上任意一点,延长PA到E,使AE=AP,以PE、PB为边作平行四边形PBQE,请问对角线PQ的长是否存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.

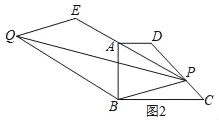
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:矩形ABCD中AB=2,BC= ![]() ,⊙A是以A为圆心,半径r=1的圆,若⊙A绕着点B顺时针旋转,旋转角为α( 0°<α<180°);当旋转后的圆与矩形ABCD的边相切时,α=度.
,⊙A是以A为圆心,半径r=1的圆,若⊙A绕着点B顺时针旋转,旋转角为α( 0°<α<180°);当旋转后的圆与矩形ABCD的边相切时,α=度. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABO的三个顶点的坐标分别为O(0,0),A(5,0),B(2,4).
(1)求△OAB的面积;
(2)若O,A两点的位置不变,P点在什么位置时,△OAP的面积是△OAB面积的2倍?
(3)若B(2,4),O(0,0)不变,M点在x轴上,M点在什么位置时,△OBM的面积是△OAB面积的2倍?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,下列说法:①∠APE=∠C,② AQ=BQ,③BP=2PQ, ④AE+BD=AB,其正确的个数有( )个.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某巡警车在一条南北大道上巡逻,某天巡警车从岗亭![]() 处出发,规定向北方向为正,当天行驶纪录如下(单位:千米)
处出发,规定向北方向为正,当天行驶纪录如下(单位:千米)
﹣10,﹣9,+7,﹣15,+6,﹣5,+4,﹣2
![]()
(1)最终巡警车是否回到岗亭![]() 处?若没有,在岗亭何方,距岗亭多远?
处?若没有,在岗亭何方,距岗亭多远?
(2)摩托车行驶1千米耗油0.2升,油箱有油10升,够不够?若不够,途中还需补充多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)已知二次函数y=ax2+bx+1的图象经过点(1,3)和(3,﹣5),求a、b的值;
(2)已知二次函数y=﹣x2+bx+c的图象与x轴的两个交点的横坐标分别为1和2.求这个二次函数的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com