
| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(吨/辆) | 5 | 8 | 10 |
| 汽车运费(元/辆) | 400 | 500 | 600 |
分析 (1)设需甲车x辆,乙车y辆列出方程组即可.
(2)设甲车有a辆,乙车有b辆,则丙车有(14-a-b)辆,列出等式.
解答 解:(1)设需甲车x辆,乙车y辆,根据题意得
$\left\{\begin{array}{l}{5x+8y=120}\\{400x+500y=8200}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=8}\\{y=10}\end{array}\right.$.
答:需甲种车型为8辆,乙种车型为10辆.
(2)设甲车有a辆,乙车有b辆,则丙车有(14-a-b)辆,由题意得
5a+8b+10(14-a-b)=120,
化简得5a+2b=20,
即a=4-$\frac{2}{5}$b,
∵a、b、14-a-b均为正整数,
∴b只能等于5,从而a=2,14-a-b=7,
∴甲车2辆,乙车5辆,丙车7辆,
∴需运费400×2+500×5+600×7=7500(元).
答:甲车2辆,乙车5辆,丙车7辆,需运费7500元.
点评 本题考查二元一次方程组的应用,一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出方程即可求解.利用整体思想和未知数的实际意义通过筛选法可得到未知数的具体解,这种方法要掌握.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
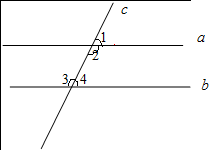 如图,因为a∥b,所以∠1=∠4,理由是两直线平行,同位角相等.
如图,因为a∥b,所以∠1=∠4,理由是两直线平行,同位角相等.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 ∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,试判断OD与OE的夹角为( )度.
∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,试判断OD与OE的夹角为( )度.| A. | 60° | B. | 65° | C. | 90° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com