
”¾ĢāÄæ”æŌĶĮÓėÓ¦ÓĆ£ŗĶ¬Ń§ĆĒ£¬ÄćĆĒŅŃ¾ÖŖµĄ![]() £¬¼“
£¬¼“![]() £®ĖłŅŌ
£®ĖłŅŌ![]() £Øµ±ĒŅ½öµ±
£Øµ±ĒŅ½öµ±![]() Ź±Č”µČŗÅ£©£®
Ź±Č”µČŗÅ£©£®
ŌĶĮ1£ŗČō![]() ĪŖŹµŹż£¬ĒŅ
ĪŖŹµŹż£¬ĒŅ![]() £Øµ±ĒŅ½öµ±
£Øµ±ĒŅ½öµ±![]() Ź±Č”µČŗÅ£©£®
Ź±Č”µČŗÅ£©£®
ŌĶĮ2£ŗČōŗÆŹż![]() £Ø
£Ø![]() £¬
£¬![]() £¬
£¬![]() ĪŖ³£Źż£©£®ÓÉŌĶĮ1½įĀŪæÉÖŖ£ŗ
ĪŖ³£Źż£©£®ÓÉŌĶĮ1½įĀŪæÉÖŖ£ŗ![]() ¼“
¼“![]() £¬”ąµ±
£¬”ąµ±![]() ¼“
¼“![]() Ź±£¬ŗÆŹż
Ź±£¬ŗÆŹż![]() µÄ×īŠ”ÖµĪŖ
µÄ×īŠ”ÖµĪŖ![]() £®
£®
ŌĶĮĄķ½āÉĻŹöÄŚČŻ£¬½ā“šĻĀĮŠĪŹĢā£ŗ
ĪŹĢā1£ŗČōŗÆŹż![]() £¬Ōņ
£¬Ōņ![]() = Ź±£¬ŗÆŹż
= Ź±£¬ŗÆŹż![]() µÄ×īŠ”ÖµĪŖ £®
µÄ×īŠ”ÖµĪŖ £®
ĪŹĢā2£ŗŅŃÖŖŅ»øö¾ŲŠĪµÄĆ껿ĪŖ4£¬ĘäÖŠŅ»±ß³¤ĪŖ![]() £¬ŌņĮķŅ»±ß³¤ĪŖ
£¬ŌņĮķŅ»±ß³¤ĪŖ![]() £¬Öܳ¤ĪŖ
£¬Öܳ¤ĪŖ![]() £¬Ēóµ±
£¬Ēóµ±![]() Ź±£¬¾ŲŠĪÖܳ¤µÄ×īŠ”ÖµĪŖ £®
Ź±£¬¾ŲŠĪÖܳ¤µÄ×īŠ”ÖµĪŖ £®
ĪŹĢā3£ŗĒ󓜏żŹ½![]() µÄ×īŠ”Öµ£®
µÄ×īŠ”Öµ£®
ĪŹĢā4£ŗ½ØŌģŅ»øöČŻ»żĪŖ8Į¢·½Ć×£¬Éī2Ć׵ij¤·½ĢåĪŽøĒĖ®³Ų£¬³Ųµ×ŗĶ³Ų±ŚµÄŌģ¼Ū·Ö±šĪŖĆæĘ½·½Ć×![]() Ć×£¬Ė®³Ų×ÜŌģ¼ŪĪŖ
Ć×£¬Ė®³Ų×ÜŌģ¼ŪĪŖ![]() £ØŌŖ£©£¬Ēóµ±
£ØŌŖ£©£¬Ēóµ±![]() ĪŖ¶ąÉŁŹ±£¬Ė®³Ų×ÜŌģ¼Ū
ĪŖ¶ąÉŁŹ±£¬Ė®³Ų×ÜŌģ¼Ū![]() ×īµĶ£æ×īµĶŹĒ¶ąÉŁ£æ
×īµĶ£æ×īµĶŹĒ¶ąÉŁ£æ
”¾“š°ø”æĪŹĢā1£ŗ![]() £»
£»![]() ĪŹĢā2£ŗ
ĪŹĢā2£ŗ![]() £»
£»![]() ĪŹĢā3£ŗ
ĪŹĢā3£ŗ![]() ĪŹĢā4£ŗµ±
ĪŹĢā4£ŗµ±![]() Ź±£¬Ė®³Ų×ÜŌģ¼Ū
Ź±£¬Ė®³Ų×ÜŌģ¼Ū![]() ×īµĶ£¬×īµĶĪŖ
×īµĶ£¬×īµĶĪŖ![]() ŌŖ
ŌŖ
”¾½āĪö”æ
ĪŹĢā1£ŗøł¾ŻŌĶĮ²ÄĮĻ½ā¾öĪŹĢā¼“æÉ£»
ĪŹĢā2£ŗøł¾Ż¾ŲŠĪµÄŠŌÖŹŗĶŌĶĮ²ÄĮĻÄŚČŻ½ųŠŠ¼ĘĖć¼“æÉĒó½ā£»
ĪŹĢā3£ŗĻČ½«“śŹżŹ½±äŠĪ£¬ŌŁøł¾ŻŌĶĮÄŚČŻ¼“æÉĒó½ā£»
ĪŹĢā4£ŗøł¾ŻĮ¢·½ĢåµÄĢå»ż¹«Ź½ŗĶŅŃÖŖĢõ¼ž±ķŹ¾³ö³¤·½ĢåµÄæķ£¬ŌĖÓĆŌĶĮÄŚČŻ¼“æÉĒó½ā£®
½ā£ŗĪŹĢā1£ŗ”ß![]()
”ą![]()
”ąÓÉŌĶĮ2½įĀŪæÉÖŖ£¬![]() ¼“
¼“![]()
”ąµ±![]() ¼“
¼“![]()
”ą![]() £¬
£¬![]() £Ø²»ŗĻĢāŅāÉįČ„£©
£Ø²»ŗĻĢāŅāÉįČ„£©
”ąµ±![]() Ź±£¬ŗÆŹż
Ź±£¬ŗÆŹż![]() µÄ×īŠ”ÖµĪŖ
µÄ×īŠ”ÖµĪŖ![]() £»
£»
ĪŹĢā2£ŗÉč¾ŲŠĪÖܳ¤ĪŖ![]() £¬øł¾ŻĢāŅāµĆ
£¬øł¾ŻĢāŅāµĆ![]()
ӧ![]()
”ą![]()
”ąµ±![]() ¼“
¼“![]() £Ø²»ŗĻĢāŅāÉįČ„£©£¬
£Ø²»ŗĻĢāŅāÉįČ„£©£¬![]() Ź±£¬ŗÆŹż
Ź±£¬ŗÆŹż![]() ÓŠ×īŠ”Öµ
ÓŠ×īŠ”Öµ![]() £»
£»
ĪŹĢā3£ŗ”ßÉč![]()
”ą![]()
ӧ![]()
”ąµ±![]() ¼“
¼“![]() £Ø²»ŗĻĢāŅāÉįČ„£©£¬
£Ø²»ŗĻĢāŅāÉįČ„£©£¬![]() Ź±£¬ŗÆŹż
Ź±£¬ŗÆŹż![]() ÓŠ×īŠ”Öµ
ÓŠ×īŠ”Öµ![]()
”ą“śŹżŹ½![]() µÄ×īŠ”ÖµĪŖ
µÄ×īŠ”ÖµĪŖ![]() £»
£»
ĪŹĢā4£ŗ”ßøł¾ŻĢāŅāµĆ³¤·½ĢåµÄæķĪŖ![]() Ć×
Ć×
”ą![]()
ӧ![]()
”ąµ±![]() ¼“
¼“![]() £Ø²»ŗĻĢāŅāÉįČ„£©£¬
£Ø²»ŗĻĢāŅāÉįČ„£©£¬![]() Ź±£¬ŗÆŹż
Ź±£¬ŗÆŹż![]() µÄ×īŠ”ÖµĪŖ
µÄ×īŠ”ÖµĪŖ![]()
”ąµ±![]() Ź±£¬Ė®³Ų×ÜŌģ¼Ū
Ź±£¬Ė®³Ų×ÜŌģ¼Ū![]() ×īµĶ£¬×īµĶĪŖ
×īµĶ£¬×īµĶĪŖ![]() ŌŖ£®
ŌŖ£®
¹Ź“š°øŹĒ£ŗĪŹĢā1£ŗ![]() £»
£»![]() ĪŹĢā2£ŗ
ĪŹĢā2£ŗ![]() £»
£»![]() ĪŹĢā3£ŗ
ĪŹĢā3£ŗ![]() ĪŹĢā4£ŗµ±
ĪŹĢā4£ŗµ±![]() Ź±£¬Ė®³Ų×ÜŌģ¼Ū
Ź±£¬Ė®³Ų×ÜŌģ¼Ū![]() ×īµĶ£¬×īµĶĪŖ
×īµĶ£¬×īµĶĪŖ![]() ŌŖ
ŌŖ


 ĆūŠ£æĪĢĆĻµĮŠ“š°ø
ĆūŠ£æĪĢĆĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖA(£4£¬n)”¢B(3£¬4)ŹĒŅ»“ĪŗÆŹży1£½kx£«bµÄĶ¼ĻóÓė·“±ČĄżŗÆŹż![]() µÄĶ¼ĻóµÄĮ½øö½»µć£¬¹żµćD(t£¬0)£Ø0£¼t£¼3£©×÷xÖįµÄ“¹Ļߣ¬·Ö±š½»Ė«ĒśĻß
µÄĶ¼ĻóµÄĮ½øö½»µć£¬¹żµćD(t£¬0)£Ø0£¼t£¼3£©×÷xÖįµÄ“¹Ļߣ¬·Ö±š½»Ė«ĒśĻß![]() ŗĶÖ±Ļßy1£½kx£«bÓŚP”¢QĮ½µć
ŗĶÖ±Ļßy1£½kx£«bÓŚP”¢QĮ½µć
(1) Ö±½ÓŠ“³ö·“±ČĄżŗÆŹżŗĶŅ»“ĪŗÆŹżµÄ½āĪöŹ½
(2) µ±tĪŖŗĪÖµŹ±£¬S”÷BPQ£½![]() S”÷APQ
S”÷APQ
(3) ŅŌPQĪŖ±ßŌŚÖ±ĻßPQµÄÓŅ²ą×÷Õż·½ŠĪPQMN£¬ŹŌĖµĆ÷£ŗ±ßQMÓėĖ«ĒśĻß![]() £Øx£¾0£©Ź¼ÖÕÓŠ½»µć
£Øx£¾0£©Ź¼ÖÕÓŠ½»µć

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹży=-x2+mx+m+1£ØĘäÖŠmĪŖ³£Źż£©
£Ø1£©øĆŗÆŹżµÄĶ¼ĻóÓėXÖį¹«¹²µćµÄøöŹżŹĒ______øö
£Ø2£©ČōøĆŗÆŹżµÄĶ¼ĻóµÄ¶Ō³ĘÖįŹĒÖ±ĻßX=1£¬¶„µćĪŖµćA£¬Ēó“ĖŹ±ŗÆŹżµÄ½āĪöŹ½¼°µćµÄ×ų±ź.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬”ĻACB=90”ć£¬DŹĒAB±ßÉĻŅ»µć£¬ŅŌBDĪŖÖ±¾¶µÄ”ŃOÓė±ßACÓŠ¹«¹²µćE£¬Į¬½įDE²¢ŃÓ³¤£¬ÓėBCµÄŃÓ³¤Ļß½»ÓŚµćF £¬BD=BF£®
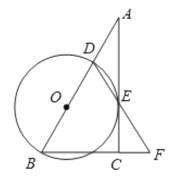
£Ø1£©ĒóÖ¤£ŗACŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©Čō”ĻF=60”ć£¬BF=8£¬ĒóCFµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABCDµÄ¶Ō½ĒĻßAC”¢BD½»ÓŚµćO£¬AEĘ½·Ö”ĻBAD½»BCÓŚµćE£¬ĒŅ”ĻADC=60”ć£¬AB=![]() BC£¬Į¬½ÓOE£®ĻĀĮŠ½įĀŪ£ŗ¢Ł”ĻCAD=30”ć£»¢ŚSABCD=ABAC£»¢ŪOB=AB£»¢ÜOE=
BC£¬Į¬½ÓOE£®ĻĀĮŠ½įĀŪ£ŗ¢Ł”ĻCAD=30”ć£»¢ŚSABCD=ABAC£»¢ŪOB=AB£»¢ÜOE=![]() BC£¬³ÉĮ¢µÄøöŹżÓŠ£Ø””””£©
BC£¬³ÉĮ¢µÄøöŹżÓŠ£Ø””””£©

A. 1øö B. 2øö C. 3øö D. 4øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµ![]() ÖŠ£¬¶ŌÓŚµć
ÖŠ£¬¶ŌÓŚµć![]() ŗĶµć
ŗĶµć![]() øų³öČēĻĀ¶ØŅå£ŗČō
øų³öČēĻĀ¶ØŅå£ŗČō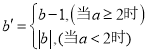 £¬Ōņ³Ęµć
£¬Ōņ³Ęµć![]() ĪŖµć
ĪŖµć![]() µÄĻŽ±äµć£®ĄżČē£ŗµć
µÄĻŽ±äµć£®ĄżČē£ŗµć![]() µÄĻŽ±äµćµÄ×ų±źŹĒ
µÄĻŽ±äµćµÄ×ų±źŹĒ![]() µć
µć![]() µÄĻŽ±äµćµÄ×ų±źŹĒ
µÄĻŽ±äµćµÄ×ų±źŹĒ![]() µć
µć![]() µÄĻŽ±äµćµÄ×ų±źŹĒ
µÄĻŽ±äµćµÄ×ų±źŹĒ![]() £®
£®
![]() ¢Łµć
¢Łµć![]() µÄĻŽ±äµćµÄ×ų±źŹĒ £»
µÄĻŽ±äµćµÄ×ų±źŹĒ £»
¢ŚŌŚµć![]() ÖŠÓŠŅ»øöµćŹĒĖ«ĒśĻß
ÖŠÓŠŅ»øöµćŹĒĖ«ĒśĻß![]() ÉĻijŅ»øöµćµÄĻŽ±äµć£¬ÕāøöµćŹĒ(Ģī”°
ÉĻijŅ»øöµćµÄĻŽ±äµć£¬ÕāøöµćŹĒ(Ģī”°![]() ”±»ņ”°
”±»ņ”°![]() ”±)
”±)
![]() Čōµć
Čōµć![]() ŌŚ¹ŲÓŚ
ŌŚ¹ŲÓŚ![]() µÄ¶ž“ĪŗÆŹż
µÄ¶ž“ĪŗÆŹż![]() µÄĶ¼ĻóÉĻ£¬ĘäĻŽ±äµć
µÄĶ¼ĻóÉĻ£¬ĘäĻŽ±äµć![]() µÄׯ×ų±ź
µÄׯ×ų±ź![]() µÄȔֵ·¶Ī§ŹĒ
µÄȔֵ·¶Ī§ŹĒ![]() »ņ
»ņ![]() ĘäÖŠ
ĘäÖŠ![]() £®Įī
£®Įī![]() £¬Ö±½ÓŠ“³ö
£¬Ö±½ÓŠ“³ö![]() µÄÖµ£®
µÄÖµ£®
![]() Čōµć
Čōµć![]() ŌŚŗÆŹż
ŌŚŗÆŹż![]() µÄĶ¼ĻóÉĻ£¬ĘäĻŽ±äµć
µÄĶ¼ĻóÉĻ£¬ĘäĻŽ±äµć![]() µÄׯ×ų±ź
µÄׯ×ų±ź![]() µÄȔֵ·¶Ī§ŹĒ
µÄȔֵ·¶Ī§ŹĒ![]() £¬Ö±½ÓŠ“³ö
£¬Ö±½ÓŠ“³ö![]() µÄȔֵ·¶Ī§£»
µÄȔֵ·¶Ī§£»
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£ĪŖĮĖĮĖ½ā¾ÅÄź¼¶Ń§ÉśĢåÓż²āŹŌ³É¼ØĒéæö£¬ŅŌ¾ÅÄź¼¶£Ø1£©°ąŃ§ÉśµÄĢåÓż²āŹŌ³É¼ØĪŖŃł±¾£¬°“B”¢C”¢DĖÄøöµČ¼¶½ųŠŠĶ³¼Ę£¬²¢½«Ķ³¼Ę½į¹ū»ęÖĘČēĻĀĮ½·łĶ³¼ĘĶ¼£¬ĒėÄć½įŗĻĶ¼ÖŠĖłøųŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ£ØĖµĆ÷£ŗA¼¶£ŗ90·Ö©100·Ö£»B¼¶£ŗ75·Ö©89·Ö£»C¼¶£ŗ60·Ö”«74·Ö£»D¼¶£ŗ60·ÖŅŌĻĀ£©
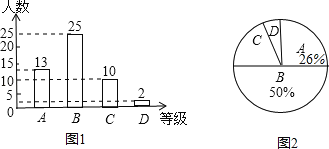
£Ø1£©Ēó³öD¼¶Ń§ÉśµÄČĖŹżÕ¼Č«°ą×ÜČĖŹżµÄ°Ł·Ö±Č£»
£Ø2£©Ēó³öÉČŠĪĶ³¼ĘĶ¼£ØĶ¼2£©ÖŠC¼¶ĖłŌŚµÄÉČŠĪŌ²ŠÄ½ĒµÄ¶ČŹż£»
£Ø3£©ČōøĆŠ£¾ÅÄź¼¶Ń§Éś¹²ÓŠ500ČĖ£¬ĒėÄć¹Ą¼ĘÕā“Īæ¼ŹŌÖŠA¼¶ŗĶB¼¶µÄѧɜ¹²ÓŠ¶ąÉŁČĖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ°ĖÄź¼¶£Ø1£©°ąŃŠ¾æŠŌѧĻ°Š”×éĪŖŃŠ¾æČ«Š£Ķ¬Ń§æĪĶāŌĶĮĒéæö£¬ŌŚČ«Š£Ė껜ŃūĒėĮĖ²æ·ÖĶ¬Ń§²ĪÓėĪŹ¾ķµ÷²é£¬Ķ³¼ĘĶ¬Ń§ĆĒŅ»øöŌĀŌĶĮæĪĶāŹéµÄŹżĮ棬²¢»ęÖĘĮĖČēĻĀµÄĶ³¼ĘĶ¼1ŗĶĶ¼2£¬Ēėøł¾ŻĶ¼ÖŠĻą¹ŲŠÅĻ¢£¬½ā¾öĻĀĮŠĪŹĢā£ŗ

£Ø¢ń£©Ķ¼1ÖŠ![]() µÄÖµĪŖ____________£¬¹²ÓŠ____________ĆūĶ¬Ń§²ĪÓėĪŹ¾ķµ÷²é£»
µÄÖµĪŖ____________£¬¹²ÓŠ____________ĆūĶ¬Ń§²ĪÓėĪŹ¾ķµ÷²é£»
£Ø¢ņ£©ĒóĶ³¼ĘµÄÕā×鏿¾ŻµÄĘ½¾łŹż”¢ÖŚŹżŗĶÖŠĪ»Źż£»
£Ø¢ó£©Č«Š£¹²ÓŠŃ§Éś1500ČĖ£¬øł¾ŻŃł±¾Źż¾Ż£¬¹Ą¼ĘøĆŠ£Ń§ÉśŅ»øöŌĀŌĶĮ2±¾æĪĶāŹéµÄČĖŹżŌ¼ĪŖ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬![]() µÄ°ė¾¶ĪŖ2£¬ĻŅ
µÄ°ė¾¶ĪŖ2£¬ĻŅ![]() £¬µćPĪŖÓÅ»”ABÉĻŅ»¶Æµć£¬
£¬µćPĪŖÓÅ»”ABÉĻŅ»¶Æµć£¬![]() £¬½»Ö±ĻßPBÓŚµćC£¬Ōņ
£¬½»Ö±ĻßPBÓŚµćC£¬Ōņ![]() µÄ×ī“óĆ껿ŹĒ
µÄ×ī“óĆ껿ŹĒ![]()
![]()
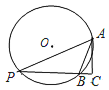
A.![]() B.1C.2D.
B.1C.2D.![]()
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com