
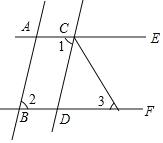
【题目】如图,已知AB∥CD,∠1=∠2,CF平分∠DCE.
(1)试判断直线AC与BD有怎样的位置关系?并说明理由;
(2)若∠1=80°,求∠3的度数.
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,沿折线ABCD方向以3cm/s的速度匀速运动;点Q从点D出发,沿线段DC方向以2cm/s的速度匀速运动. 已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为t(s).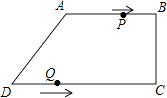
(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲所示,若将阴影两部分裁剪下来重新拼成一个正方形,所拼正方形如图乙.

![]() 图甲的长是______,宽是______,面积是______
图甲的长是______,宽是______,面积是______![]() 写成两式乘积形式
写成两式乘积形式![]() ;如图乙所示,阴影部分的面积是______
;如图乙所示,阴影部分的面积是______![]() 写成多项式的形式
写成多项式的形式![]()
![]() 比较图甲和图乙中阴影部分的面积,可得乘法公式______.
比较图甲和图乙中阴影部分的面积,可得乘法公式______.
![]() 运用你所得到的公式,计算下列各题:
运用你所得到的公式,计算下列各题:
![]() ;
;
![]() ;
;
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() ;
;
(2)先化简![]() ,再选一个你喜欢的数求值.
,再选一个你喜欢的数求值.
(1)(﹣2016)0+| ![]() ﹣2|+
﹣2|+ ![]() +3tan30°
+3tan30°
(2)先化简(a2﹣a)÷ ![]() ,再选一个你喜欢的数求值.
,再选一个你喜欢的数求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“佳佳商场”在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,“佳佳商场”应将这种商品的售价定为多少?
(2)物价局规定该商品的售价不能超过40元/件,“佳佳商场”为了获得最大的利润,应将该商品售价定为多少?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE. 
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义正整数m,n的运算,m△n=![]()
例2△3=![]() ,3△4=
,3△4=![]()
(1)3△2的值为 运算符号“△”满足交换律吗?回答 (填“是”或者“否”)
(2)探究:计算2△10=![]() 的值.
的值.
为解决上面的问题,我们运用数形结合的思想方法,通过不断的分割一个面积为1的正方形,把数量关系和几何图形结合起来,最终解决问题.
如图所示,第1次分割把正方形的面积二等分,其中阴影部分的面积为![]() ,第2次,把上次分割图中空白部分的面积继续二等分,阴影分的面积之和为
,第2次,把上次分割图中空白部分的面积继续二等分,阴影分的面积之和为![]() ,第3次分割把上次分割图中空白部分的面积继续二等分……以此类推……第10次分割,把第9次分割后的图中的空日部分的面积最后二等分,所有阴影部分面积之和为
,第3次分割把上次分割图中空白部分的面积继续二等分……以此类推……第10次分割,把第9次分割后的图中的空日部分的面积最后二等分,所有阴影部分面积之和为![]() .
.
根据第10次分割图可以得出计结果:![]() =1﹣
=1﹣![]() ,进一步分析可得出
,进一步分析可得出![]() =1﹣
=1﹣![]() ,
,

(3)已知n是正整数,计算3×(4△n)=![]() 的结果.
的结果.
按指定方法解决问题请仿照以上做法,只需画出第n次分割图并作标注,写出最终结果的推理步骤,或借用以上结论进行推理,写出必要的步骤.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形OABC的边OC、OA分别在x、y轴的正半轴上,点B坐标为(10,10),点P从O出发沿O→C→B运动,速度为1个单位每秒,连接AP.设运动时间为t.
(1)若抛物线y=﹣(x﹣h)2+k经过A,B两点,求抛物线函数关系式;
(2)当0≤t≤10时,如图1,过点O作OH⊥AP于点H,直线OH交边BC于点D,连接AD,PD,设△APD的面积为S,求S的最小值;
(3)在图2中以A为圆心,OA长为半径作⊙A,当0≤t≤20时,过点P作PQ⊥x轴(Q在P的上方),且线段PQ=t+12:
①当t在什么范围内,线段PQ与⊙A只有一个公共点?当t在什么范围内,线段PQ与⊙A有两个公共点?
②请将①中求得的t的范围作为条件,证明:当t取该范围内任何值时,线段PQ与⊙A总有两个公共点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游的人数x(人)之间的函数关系.
(1)当参加旅游的人数不超过10人时,人均收费为元;
(2)如果该公司支付给旅行社3600元,那么参加这次旅游的人数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com