
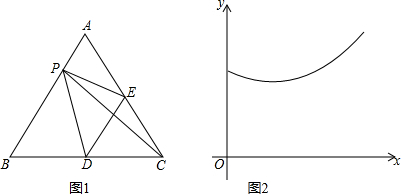
| A. | 线段PE | B. | 线段PD | C. | 线段PC | D. | 线段DE |
分析 设出等边三角形的边长,根据等边三角形的性质确定各个线段取最小值时,x的范围,结合图象得到答案.
解答 解:设等边三角形边长为1,则0≤x≤1,
如图1,分别过点E、C、D作AB的垂线,垂足分别为F、G、H,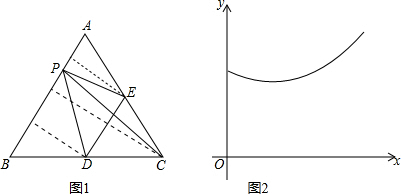
根据等边三角形的性质可知,
当x=$\frac{1}{4}$时,线段PE有最小值;
当x=$\frac{1}{2}$时,线段PC有最小值;
当x=$\frac{3}{4}$时,线段PD有最小值;
∵点E、D分别是AC,BC边的中点
∴线段DE的长为定值$\frac{1}{2}$.
根据图2可知,当x=$\frac{1}{4}$时,函数有最小值,故这条线段为PE.
故选A.
点评 本题主要考查的是动点问题的函数图象,灵活运用等边三角形的性质和二次函数图象的对称性是解题的关键.解题时需要深刻理解动点的函数图象,了解图象中关键点所代表的实际意义.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
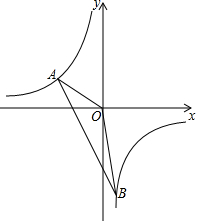 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(-3,m+8),B(n,-6)两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(-3,m+8),B(n,-6)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好的了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩,
为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好的了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩,| 成绩/分 | 频数 | 频率 |
| 50≤x<60 | 10 | 0.05 |
| 60≤x<70 | 20 | 0.10 |
| 70≤x<80 | 30 | b |
| 80≤x<90 | a | 0.30 |
| 90≤x≤100 | 80 | 0.40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
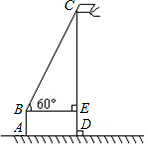 小明周日在广场放风筝,如图,小明为了计算风筝离地面的高度,他测得风筝的仰角为60°,已知风筝线BC的长为20米,小明的身高AB为1.75米,请你帮小明计算出风筝离地面的高度.(结果精确到0.1米,参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
小明周日在广场放风筝,如图,小明为了计算风筝离地面的高度,他测得风筝的仰角为60°,已知风筝线BC的长为20米,小明的身高AB为1.75米,请你帮小明计算出风筝离地面的高度.(结果精确到0.1米,参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
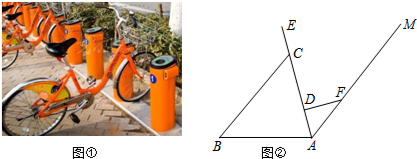
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com