
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 的坐标为(0,2),点
的坐标为(0,2),点![]() 是
是![]() 上一动点,连接
上一动点,连接![]() ,将
,将![]() 绕
绕![]() 点逆时针旋转90°得到线段
点逆时针旋转90°得到线段![]() ,使点
,使点![]() 恰好落在
恰好落在![]() 上,则点
上,则点![]() 的坐标为______.
的坐标为______.

【答案】(2,6)
【解析】
过点D作DE⊥OA于E,根据旋转的性质可得CD=DP,根据同角的余角相等求出∠OPC=∠ECD,再利用“角角边”证明△OCP和△EDC全等,根据全等三角形对应边相等可得DE=OC,CE=OP,再求出OE,然后写出点D的坐标即可.
如图,过点D作DE⊥OA于E,
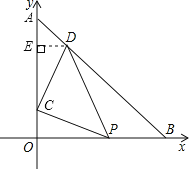
∵CP绕C点逆时针旋转90°得到线段CD,
∴CD=DP,
∵旋转角为90°,
∴∠PCD=90°,
∴∠ECD+∠OCP=90°,
又∵∠OPC+∠OCP=90°,
∴∠OPC=∠ECD,
在△OCP和△EDC中,
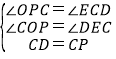 ,
,
∴△OCP≌△EDC(AAS),
∴DE=OC=2,
∵点D在AB上,△AOB∽△AED,而OA=OB=9,
∴AE=DE=2,
∴OE=OA-AE=8-2=6.
∴点D的坐标为(2,6).


科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC与BD交于点O,下列各组条件,其中不能判定四边形ABCD是平行四边形的是( )
A. OA=OC,OB=ODB. OA=OC,AB∥CD
C. AB=CD,OA=OCD. ∠ADB=∠CBD,∠BAD=∠BCD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果过抛物线![]() 与y的交点作y轴的垂线与该抛物线有另一个交点,并且这两点与该抛物线的顶点构成正三角形,那么我们称这个抛物线为正三角抛物线.
与y的交点作y轴的垂线与该抛物线有另一个交点,并且这两点与该抛物线的顶点构成正三角形,那么我们称这个抛物线为正三角抛物线.
(1)抛物线![]() 正三角抛物线;(填“是”或“不是”)
正三角抛物线;(填“是”或“不是”)
(2)如图,已知二次函数![]() (m > 0)的图像是正三角抛物线,它与x轴交于A、B两点(点A在点B的左侧),点E在y轴上,当∠AEB=2∠ABE时,求出点E的坐标.
(m > 0)的图像是正三角抛物线,它与x轴交于A、B两点(点A在点B的左侧),点E在y轴上,当∠AEB=2∠ABE时,求出点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝重庆八中建校八十周年,学校要举行一系列的庆祝活动. 庆祝活动的主要方式有四种,分别是A:“我与八中同成长”诗歌征文比赛、B:“舞动八中”街舞比赛、C:“水墨校园”绘画比赛、D:“历史名人cosplay”比赛. 学校围绕“你最喜欢的活动方式是什么?”在全校学生中随机抽样部分学生进行调查(四个选项中必须且只选一项),根据调查统计结果,绘制了如下两种不完整的统计图表:


“最喜欢的活动方式”条形统计图 “最喜欢的活动方式”扇形统计图
(1)本次抽查的学生共_______人,m=__________,并将条形统计图补充完成;
(2)学校采用抽签方式让每班在A,B,C,D四项宣传方式中随机抽取两项进行展示,请用树状图或列表法求某班所抽到的两项方式恰好是A和B的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对七年级全体学生进行了期中测试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了下面的条形图和扇形图(图1和图2均不完整)请根据图中所给的信息,解答下列问题:
(1)求抽取学生的人数,请将表示成绩类别为“中”的条形图补充完整;
(2)求扇形图中表示成绩类别为“优“的扇形所占的百分数;
(3)如果该校七年级共有300人参加期中测试,请估计成绩在“良”及“良”以上的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于两个两位数m和n,将其中任意一个两位数的十位上的数字和个位上的数字分别放置于另一个两位数十位上数字与个位上的数字之间和个位上的数字的右边,就可以得到两个新四位数,把这两个新四位数的和与11的商记为F(m,n)。例如:当m=36,n=10时,将m十位上的3放置n中1与0之间,将m个位上的6位置于n中0的右边,得到1306.将n个十位上的1放置于m中3和6之间,将n个位上的0放置于m中6的右边,得到3160。这两个新四位数的和为1306+3160=4466,4466÷11=406,所以F(36,10)=406。
(1)计算:F(20,18);
(2)若a=10+x,b=10y+8(0≤x≤9,1≤y≤9,x,y都是自然数)。当150 F(a,36)+ F(b,49)=62767时,求F(5a,b)的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,某超市对出售![]() 、
、![]() 两种商品开展元旦促销活动,活动方案有如下两种:(同一种商品不可同时参与两种活动)
两种商品开展元旦促销活动,活动方案有如下两种:(同一种商品不可同时参与两种活动)
商品 |
|
| |
标价(单位:元) |
|
| |
方案一 | 每件商品出售价格 | 按标价降价 | 按标价降价 |
方案二 | 若所购商品超过 | ||
(1)某单位购买![]() 商品
商品![]() 件,
件,![]() 商品
商品![]() 件,共花费
件,共花费![]() 元,试求
元,试求![]() 的值;
的值;
(2)在(1)求出的![]() 值的条件下,若某单位购买
值的条件下,若某单位购买![]() 商品
商品![]() 件(
件(![]() 为正整数),购买
为正整数),购买![]() 商品的件数比
商品的件数比![]() 商品件数的
商品件数的![]() 倍还多一件,请问该单位选择哪种方案才能获得最大优惠?请说明理由.
倍还多一件,请问该单位选择哪种方案才能获得最大优惠?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac<0;②当x>-1时y随x增大而减小;③a+b+c<0;④若方程ax2+bx+c-m=0没有实数根,则m>2;⑤3a+c<0.其中,正确结论的序号是________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com