
【题目】如图,反比例函数y=![]() (k>0)与矩形OABC在第一象限相交于D、E两点,OA=2,OC=4,连接OD、OE、DE.记△OAD、△OCE的面积分别为S、S .
(k>0)与矩形OABC在第一象限相交于D、E两点,OA=2,OC=4,连接OD、OE、DE.记△OAD、△OCE的面积分别为S、S .
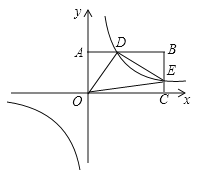
(1)①点B的坐标为 ;②S S(填“>”、“<”、“=”);
(2)当点D为线段AB的中点时,求k的值及点E的坐标;
(3)当S+S=2时,试判断△ODE的形状,并求△ODE的面积.
【答案】(1)点B的坐标为(4,2),= ;
(2)k的值为4,点E的坐标为(4,1) ;
(3)△ODE为直角三角形,![]()
【解析】
(1)根据OA=2,OC=4可直接得到点B坐标;②根据反比例函k的意义可知S1、S2都等于![]() |k|,即可得到答案;
|k|,即可得到答案;
(2)当点D为AB中点时,AD=2,得出D的坐标是(2,2),![]() ,进而可得解;
,进而可得解;
(3)根据当S1+S2=2时,由(1)得出S1=S2=1,进而得出BD,BE的长,进而得出DO2+DE2=OE2,△ODE是直角三角形,进而得出三角形面积.
(1)矩形OABC,AB=OC,BC=OA;OA=2,OC=4,B点在第一象限
所以点B的坐标为(4,2);
反比例函数y=![]() (k>0)与矩形OABC在第一象限相交于D、E两点,
(k>0)与矩形OABC在第一象限相交于D、E两点,
设D、E两点的坐标分别为![]() ,
,
得![]() ;
;
D、E在第一象限, 记△OAD、△OCE的面积分别为![]() 、
、![]() ,
,![]() ,
,
所以![]() =
=![]()
(2)当点D为线段AB的中点时,D点的坐标(2,2),由(1)知![]() ,
,
解得k=4,
![]() ,
,
所以点E的坐标为(4,1)
(3) 当![]() +S=2时,由(1)得
+S=2时,由(1)得![]() ;
;
![]() =1,
=1,![]() ;
;![]() ;
;
在矩形OABC,BD=AB-AD=3;BE=BC-CE=![]() ;
;
![]() 都是直角三角形,由勾股定理得
都是直角三角形,由勾股定理得![]()
∵![]()
∴△ODE为直角三角形,![]()
∴![]() OD·DE=
OD·DE=![]() ×
×![]() ×
×![]()
![]()


科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
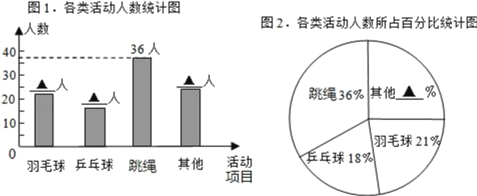
【题目】学校统筹安排大课间体育活动,在各班随机选取了一部分学生,分成四类活动:“跳绳”、“羽毛球”、“乒乓球”、“其他”进行调查,整理收集到的数据,绘制成如图的两幅统计图.
(1)学校采用的调查方式是 ;学校在各班随机选取了 名学生;
(2)补全统计图中的数据:羽毛球 人、乒乓球 人、其他 %;
(3)该校共有900名学生,请估计喜欢“跳绳”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
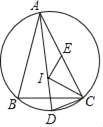
【题目】点I为△ABC的内心,连AI交△ABC的外接圆于点D,若AI=2CD,点E为弦AC的中点,连接EI,IC,若IC=6,ID=5,则IE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
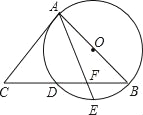
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是![]() 的中点,AE与BC交于点F,∠C=2∠EAB.
的中点,AE与BC交于点F,∠C=2∠EAB.
(1)求证:AC是⊙O的切线;
(2)已知CD=4,CA=6,
①求CB的长;
②求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
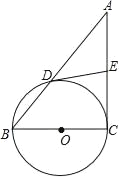
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,DE交AC于点E,且∠A=∠ADE.
(1)求证:DE是⊙O的切线;
(2)若AD=16,DE=10,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
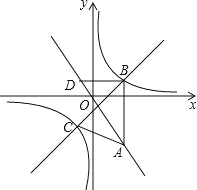
【题目】如图,在平面直角坐标系xOy中,点A(a,﹣![]() )在直线y=﹣
)在直线y=﹣![]() 上,AB∥y轴,且点B的纵坐标为1,双曲线y=
上,AB∥y轴,且点B的纵坐标为1,双曲线y=![]() 经过点B.
经过点B.
(1)求a的值及双曲线y=![]() 的解析式;
的解析式;
(2)经过点B的直线与双曲线y=![]() 的另一个交点为点C,且△ABC的面积为
的另一个交点为点C,且△ABC的面积为![]() .
.
①求直线BC的解析式;
②过点B作BD∥x轴交直线y=﹣![]() 于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com