
����Ŀ���Ķ����в��ϣ�������⣺
���壺�߶�AD�ѵ���������ABC�ֳɡ�ABD���ACD����ͼ1���������ABD���ACD��Ϊ���������Σ���ô�߶�AD������ABC�������ָ���.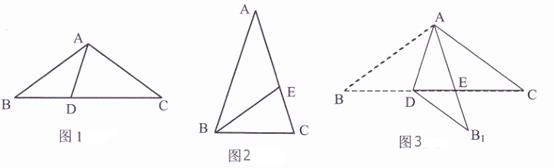
��1����ͼ1����֪��ABC�У�AB=AC����BAC=108�㣬ADΪ��ABC�������ָ��ߣ���BD<CD�����B= �� ��ADC=.
��2����ͼ2����֪��ABC�У�AB=AC����A=36�㣬BEΪ��ABC�Ľ�ƽ���ߣ���֤��BEΪ��ABC�����ָ���.
��3����ͼ3����֪��ABC��һ����������ֽƬ��AB=AC��AD������һ�������ָ��ߣ�����ABD��ֱ��AD�۵���B���ڵ�B1����AB1��CD�ڵ�E����֤��DB1=EC.
���𰸡�
��1��36o��72o
��2��
֤������AB=AC
���ABC=��C= ![]()
��BEΪ��ABC�Ľ�ƽ����
�� ![]()
���ABE=��A
��AE=BE�ߡ�BEC=180�C��C�C��CBE=72
���BEC=��C
��BE=BC
���ABE����BEC������������
��BEΪ��ABC�������ָ��ߣ�
��3��
֤������AD�ǡ�ABC��һ�������ָ���
��AD=BD��AC=CD
���B=��BAD����CAD=��CDA
�ߡ�B+��BAD+��ADB=180����ADB+��CDA=180
���CDA=��B+��BAD=2��BAD
���CAD=2��BAD
�ߡ�BAD=��B1AD
���CAD=2��B1AD
�ߡ�CAD=��B1AD+��CAE
���B1AD=��CAE
��AB=AC
���B=��C
�ߡ�B=��B1
���B1=��C
��AB=AB1
��AB1= AC
���AB1D�ա�ACE
��DB1=CE
���������⣺��1����AB=AC����BAC=108�㣬���B= ![]() =36�㣬��ADΪ��ABC�������ָ��ߣ�BD<CD����AC=AD��BD=AD�����ADC=
=36�㣬��ADΪ��ABC�������ָ��ߣ�BD<CD����AC=AD��BD=AD�����ADC= ![]() 72��.
72��.
���Դ���72��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵��:�������IJ����dz�����;�������IJ��������������;��������������ⳤ�����;�����������в��ⳤ�����.������ȷ����_____.(�����)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼΪ4��4������������ͼ�е��߶ξ�Ϊ����߶Σ��߶εĶ˵�Ϊ��㣩������1+��2+��3+��4+��5�Ķ���Ϊ__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����ѧ���ᄊ�˶����ϣ�21���μ�����������Ŀ���˶�Ա�ɼ��y�����£�
�ɼ���m�� | 1.50 | 1.55 | 1.60 | 1.65 | 1.70 |
���� | �� | 8 | 6 | �� | 1 |
�������������ݱ���ˮ�ܻ�ģ�����ˣ�����������������ȷ����ͳ�����ǣ� ��
A.ƽ����B.��λ��C.����D.����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±���ijУ�������20�����꼶����������ͳ�Ʊ���
���ߣ�cm�� | 150 | 155 | 160 | 163 | 165 | 168 |
�������ˣ� | 1 | 3 | 4 | 4 | 5 | 3 |
�������ݵ�������__cm����λ����__cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������11�֣����һ���������ܱ�һ���߶ηָ���������������Σ���ô�������߶�Ϊ��������ε������ߣ������������Ϊ���������Σ�
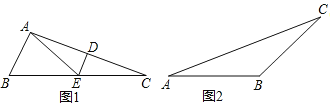
��1����ͼ1����ABC�У���B=2��C���߶�AC�Ĵ�ֱƽ���߽�AC�ڵ�D����BC�ڵ�E����֤��AE����ABC��һ�������ߣ�
��2����ͼ2������ABC�����������Σ���A=30�㣬��BΪ�۽ǣ�������п��ܵ���B�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ� ��
A.a2+a2=a4
B.����b2��3=��b6
C.2x2x2=2x3
D.��m��n��2=m2��n2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������11�֣���֪��ABC=90�㣬D��ֱ��AB�ϵĵ㣬AD=BC��
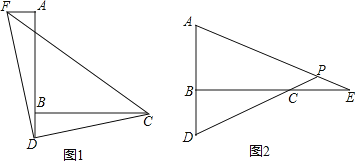
��1����ͼ1������A��AF��AB������ȡAF=BD������DC��DF��CF���ж���CDF����״��֤����
��2����ͼ2��E��ֱ��BC��һ�㣬��CE=BD��ֱ��AE��CD�ཻ�ڵ�P����APD�Ķ�����һ���̶���ֵ�����ǣ���������Ķ����������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
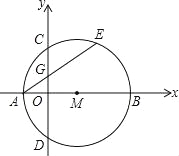
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���m��x����������ϣ���M��x����A��B���㣬��y����C��D���㣬��CΪ��AE���е㣬AE��y����G�㣬����A������Ϊ����2��0����AE=8��
��1����֤��AE=CD��
��2�����C�������Mֱ��AB�ij���
��3����OG�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com