
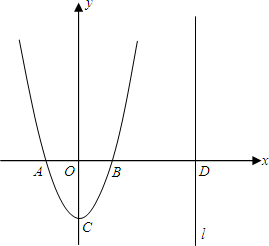
 ��2013•��������ͼ�����κ���y=ax2+bx+c��ͼ��Ķ���C������Ϊ��0��-2������x����A��B���㣬����A��-1��0����ֱ��l��x=m��m��1����x�ύ��D��
��2013•��������ͼ�����κ���y=ax2+bx+c��ͼ��Ķ���C������Ϊ��0��-2������x����A��B���㣬����A��-1��0����ֱ��l��x=m��m��1����x�ύ��D��| m-1 |
| 2 |
| OB |
| DP |
| OC |
| DB |
| 1 |
| n |
| 2 |
| m-1 |
| m-1 |
| 2 |
| m-1 |
| 2 |
| 1-m |
| 2 |
| OB |
| DB |
| OC |
| DP |
| 1 |
| m-1 |
| 2 |
| n |
| m-1 |
| 2 |
 ��ͼ������Q��QE��l�ڵ�E��
��ͼ������Q��QE��l�ڵ�E��
|
| m-1 |
| 2 |
|
|
|
|
|
|


 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д� �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2013•��������ͼ����֪����OABC�У�OA=2��AB=4��˫����y=
��2013•��������ͼ����֪����OABC�У�OA=2��AB=4��˫����y=| k | x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
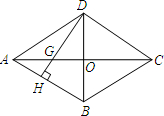 ��2013•��������ͼ���ı���ABCD�����Σ��Խ���AC=8cm��BD=6cm��DH��AB�ڵ�H����DH��AC����G����GH=��������
��2013•��������ͼ���ı���ABCD�����Σ��Խ���AC=8cm��BD=6cm��DH��AB�ڵ�H����DH��AC����G����GH=���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2013•��������ͼ��AB�ǡ�O��ֱ����C�ǰ�ԲO�ϵ�һ�㣬ACƽ�֡�DAB��AD��CD������ΪD��AD����O��E������CE��
��2013•��������ͼ��AB�ǡ�O��ֱ����C�ǰ�ԲO�ϵ�һ�㣬ACƽ�֡�DAB��AD��CD������ΪD��AD����O��E������CE�� | AC |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2013•��������ͼ��Ҫš��һ���߳�Ϊa=6mm������������ñ�������ſ��Ŀ���b����Ϊ��������
��2013•��������ͼ��Ҫš��һ���߳�Ϊa=6mm������������ñ�������ſ��Ŀ���b����Ϊ���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2013•��������ͼ������������֮����һ��ˣ���15�ף���A�㾭����˶���ǡ�ÿ������������ǽ��C�㣬�Ҹ��Ǧ�Ϊ60�㣬�ִ�A����D��ĸ��Ǧ�Ϊ30�㣬����˵�GΪBC���е㣬������ĸ�CDΪ��������
��2013•��������ͼ������������֮����һ��ˣ���15�ף���A�㾭����˶���ǡ�ÿ������������ǽ��C�㣬�Ҹ��Ǧ�Ϊ60�㣬�ִ�A����D��ĸ��Ǧ�Ϊ30�㣬����˵�GΪBC���е㣬������ĸ�CDΪ���������鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com