
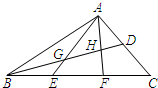
 如图,在△ABC中,AD=DC,BE=EF=FC,AE、AF与BD相交于点G、H.已知${S_{△AHD}}=\frac{3}{10}$,则S四边形GEFH的值是( )
如图,在△ABC中,AD=DC,BE=EF=FC,AE、AF与BD相交于点G、H.已知${S_{△AHD}}=\frac{3}{10}$,则S四边形GEFH的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{7}{10}$ | C. | $\frac{6}{11}$ | D. | $\frac{11}{20}$ |
分析 连接DF,根据三角形中位线定理可得DF∥AE,DF=$\frac{1}{2}$AE.然后运用相似三角形的性质得到GH、DH与DC的关系,然后运用等积变换就可得到S四边形EFHG与S△ABC的关系、S△AHD与S△ABC的关系,从而解决问题.
解答 解:连接DF,如图.
∵AD=DC,EF=FC,
∴DF∥AE,DF=$\frac{1}{2}$AE
∵GE∥DF,
∴△BGE∽△BDF,
∴$\frac{BG}{BD}$=$\frac{GE}{DF}$=$\frac{BE}{BF}$.
∵BE=EF,
∴BF=2BE,
∴BD=2BG,DF=2EG,
∴AE=2DF=4EG,
∴AG=3EG=$\frac{3}{2}$DF.
∵AG∥DF,
∴△AHG∽△FHD,
∴$\frac{HG}{HD}$=$\frac{AG}{FG}$=$\frac{3}{2}$.
设HD=2k,
则HG=3k,DG=5k,BD=2BG=2GD=10k.
∵$\frac{{S}_{△AGH}}{{S}_{△ADB}}$=$\frac{GH}{DB}$=$\frac{3}{10}$,$\frac{{S}_{△ADB}}{{S}_{△ABC}}$=$\frac{AD}{AC}$=$\frac{1}{2}$,
∴$\frac{{S}_{△AGH}}{{S}_{△ABC}}$=$\frac{3}{10}×\frac{1}{2}$=$\frac{3}{20}$,
∴S△AGH=$\frac{3}{20}$S△ABC.
∵$\frac{{S}_{△AEF}}{{S}_{△ABC}}$=$\frac{EF}{BC}$=$\frac{EF}{3EF}$=$\frac{1}{3}$,
∴S△AEF=$\frac{1}{3}$S△ABC,
∴S四边形EFHG=S△AEF-S△AGH=$\frac{1}{3}$S△ABC-$\frac{3}{20}$S△ABC=$\frac{11}{60}$S△ABC.
∵$\frac{{S}_{△ADH}}{{S}_{△ADB}}$=$\frac{DH}{BD}$=$\frac{1}{5}$,$\frac{{S}_{△ADB}}{{S}_{△ABC}}$=$\frac{AD}{AC}$=$\frac{1}{2}$,
∴$\frac{{S}_{△ADH}}{{S}_{△ABC}}$=$\frac{1}{5}$×$\frac{1}{2}$=$\frac{1}{10}$.
∵S△AHD=$\frac{3}{10}$,
∴S△ABC=3,
∴S四边形EFHG=$\frac{11}{60}$×3=$\frac{11}{20}$.
故选:D.
点评 本题主要考查了等积变换、三角形中位线定理、相似三角形的判定与性质等知识,由多中点联想到三角形的中位线定理,并运用相似三角形的性质和等积变换是解决本题的关键.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点D在双曲线y=$\frac{20}{x}$(x>0)的图象上,以D为圆心的⊙D与y轴相切于点C(0,4),与x轴交于A,B两点,抛物线y=ax2+bx+c经过A,B,C三点,点P是抛物线上的动点,且线段AP与BC所在直线有交点Q.
如图,已知点D在双曲线y=$\frac{20}{x}$(x>0)的图象上,以D为圆心的⊙D与y轴相切于点C(0,4),与x轴交于A,B两点,抛物线y=ax2+bx+c经过A,B,C三点,点P是抛物线上的动点,且线段AP与BC所在直线有交点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
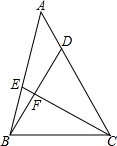 如图,在△ABC中,点D,E分别在边AC,AB上,且BD=CE=BC.若∠A=25°,则∠BFC=130°;若∠A=45°且BF:CF=5:12,则AE:AB=2:3.
如图,在△ABC中,点D,E分别在边AC,AB上,且BD=CE=BC.若∠A=25°,则∠BFC=130°;若∠A=45°且BF:CF=5:12,则AE:AB=2:3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
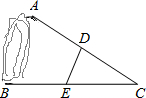 如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,通过测量分别取AC,BC的中点D和E,量得DE长210米,则A,B两点间的距离为( )
如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,通过测量分别取AC,BC的中点D和E,量得DE长210米,则A,B两点间的距离为( )| A. | 280米 | B. | 300米 | C. | 420米 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com