
【题目】如图,点C在以AB为半径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D
关AC对称,DF⊥DE于点D,并交EC的延长线与点F.下列结论:①CE=CF;②线段EF的最小值为2![]()
③当AD=2时,EF与半圆相切;④当点D从点A运动到点B时,线段EF扫过的面积是16![]() .其中正
.其中正
确的结论()

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
(1)由点E与点D关于AC对称可得CE=CD,再根据DF⊥DE即可证到CE=CF.
(2)根据“点到直线之间,垂线段最短”可得CD⊥AB时CD最小,由于EF=2CD,求出CD的最小值就可求出EF的最小值.
(3)连接OC,易证△AOC是等边三角形,AD=OD,根据等腰三角形的“三线合一”可求出∠ACD,进而可求出∠ECO=90°,从而得到EF与半圆相切.
(4)利用相似三角形的判定与性质可证到△DBF是等边三角形,只需求出BF就可求出DB,进而求出AD长.
(5)首先根据对称性确定线段EF扫过的图形,然后探究出该图形与△ABC的关系,就可求出线段EF扫过的面积.
接CD,如图1所示.

∵点E与点D关于AC对称,
∴CE=CD.
∴∠E=∠CDE.
∵DF⊥DE,
∴∠EDF=90°.
∴∠E+∠F=90°,∠CDE+∠CDF=90°.
∴∠F=∠CDF.
∴CD=CF.
∴CE=CD=CF.
∴结论“CE=CF”正确.
②当CD⊥AB时,如图2所示.

∵AB是半圆的直径,
∴∠ACB=90°.
∵AB=8,∠CBA=30°,
∴∠CAB=60°,AC=4,BC=4![]() .
.
∵CD⊥AB,∠CBA=30°,
∴CD=![]() BC=2
BC=2![]() .
.
根据“点到直线之间,垂线段最短”可得:
点D在线段AB上运动时,CD的最小值为2![]() .
.
∵CE=CD=CF,
∴EF=2CD.
∴线段EF的最小值为4![]() .
.
∴结论“线段EF的最小值为2![]() ”错误.
”错误.
③当AD=2时,连接OC,如图3所示.

∵OA=OC,∠CAB=60°,
∴△OAC是等边三角形.
∴CA=CO,∠ACO=60°.
∵AO=4,AD=2,
∴DO=2.
∴AD=DO.
∴∠ACD=∠OCD=30°.
∵点E与点D关于AC对称,
∴∠ECA=∠DCA.
∴∠ECA=30°.
∴∠ECO=90°.
∴OC⊥EF.
∵EF经过半径OC的外端,且OC⊥EF,
∴EF与半圆相切.
∴结论“EF与半圆相切”正确.
④当点F恰好落在![]()
上时,连接FB、AF,如图4所示

∵点E与点D关于AC对称,
∴ED⊥AC.
∴∠AGD=90°.
∴∠AGD=∠ACB.
∴ED∥BC.
∴△FHC∽△FDE.
∴![]() .
.
∵FC=![]() EF,
EF,
∴FH=![]() FD.
FD.
∴FH=DH.
∵DE∥BC,
∴∠FHC=∠FDE=90°.
∴BF=BD.
∴∠FBH=∠DBH=30°.
∴∠FBD=60°.
∵AB是半圆的直径,
∴∠AFB=90°.
∴∠FAB=30°.
∴FB=![]() AB=4.
AB=4.
∴DB=4.
∴AD=AB-DB=4.
∴结论“AD=2![]() ”错误.
”错误.
⑤如图所示:

∵点D与点E关于AC对称,
点D与点F关于BC对称,
∴当点D从点A运动到点B时,
点E的运动路径AM与AB关于AC对称,
点F的运动路径NB与AB关于BC对称.
∴EF扫过的图形就是图5中阴影部分.
∴S阴影=2S△ABC
=2×![]() ACBC
ACBC
=ACBC
=4×4![]()
=16![]() .
.
∴EF扫过的面积为16![]() .
.
∴结论“EF扫过的面积为16![]() ”正确.
”正确.
所以①、③、⑤正确,共计3个.
故选:C.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,线段AB=9,射线BG⊥AB,P为射线BG上一点,以AP为边作正方形APCD,且C、D与点B在AP两侧,在线段DP取一点E,使∠EAP=∠BAP,直线CE与线段AB相交于点F(点F与点A、B不重合).

(1)求证:△AEP≌△CEP;
(2)判断CF与AB的位置关系,并说明理由;
(3)求△AEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1,是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.
的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.



(1)图2中的阴影部分的面积为 ;
(2)观察图2,三个代数式![]() ,
,![]() ,
,![]() 之间的等量关系是 ;
之间的等量关系是 ;
(3)若![]() ,
,![]() ,求
,求![]() ;
;
(4)观察图3,你能得到怎样的代数恒等式呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
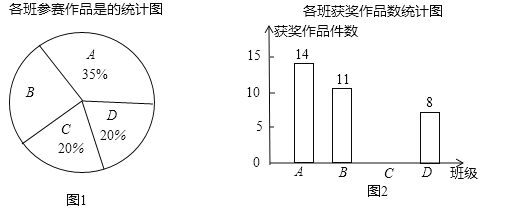
【题目】【本小题满分9分】某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中.
(1)B班参赛作品有多少件?
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高?
(4)将写有A、B、C、D四个字母的完全相同的卡片放人箱中,从中一次随机抽出两张卡片,求抽到A、B两班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
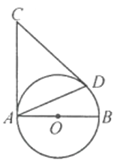
【题目】如图,CA,CD是⊙O的两条切线,切点分别为A,D,AB是⊙O的直径.
⑴ 若∠C=50°,求∠BAD的度数;
⑵ 若AB=AC=4,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=(x+m)2+m与直线y=x相交于E,C两点(点E在点C的左边),抛物线与x轴交
于A,B两点(点A在点B的左边).△ABC的外接圆⊙H与直线y=-x相交于点D.
⑴ 若抛物线与y轴交点坐标为(0,2),求m的值;
⑵ 求证:⊙H与直线y=1相切;
⑶ 若DE=2EC,求⊙H的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
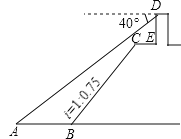
A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC ∠ACB ,BD 、CD 分别平分△ABC 的内角 ∠ABC 、外角 ∠ACP ,BE平分外角 ∠MBC 交 DC 的延长线于点 E ,以下结论:①∠BDE ![]() ∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正确的结论有( )
∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正确的结论有( )
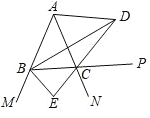
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com